Example 1: packing of super-ellipsoids
The surface function of a superellipsoid in the local Cartesian coordinates can be defined as $$\label{eqsurface} \Big(\big|\frac{x}{r_x}\big|^{\frac{2}{\epsilon_1}} + \big|\frac{y}{r_y}\big|^{\frac{2}{\epsilon_1}}\Big)^{\frac{\epsilon_1}{\epsilon_2}} + \big|\frac{z}{r_z}\big|^{\frac{2}{\epsilon_2}} = 1$$ where $r_x, r_y$ and $r_z$ are referred to as the semi-major axis lengths in the direction of x, y, and z axies, respectively; and $\epsilon_i (i=1,2)$ are the shape parameters determining the sharpness of particle edges or squareness of particle surface. Varying $\epsilon_i$ between 0 and 2 yields a wide range of convex-shaped superellipsoid. Two functions for generating a superellipsoid are highlighted below (see Sec. 5.1.2{reference-type=“ref” reference=“modsuperquadrics”}):
-
NewSuperquadrics2($r_x$, $r_y$, $r_z$, $\epsilon_1$, $\epsilon_2$, mat, rotate, isSphere)
-
NewSuperquadrics_rot2($r_x$, $r_y$, $r_z$, $\epsilon_1$, $\epsilon_2$, mat, $q_w$, $q_x$, $q_y$, $q_z$, isSphere)
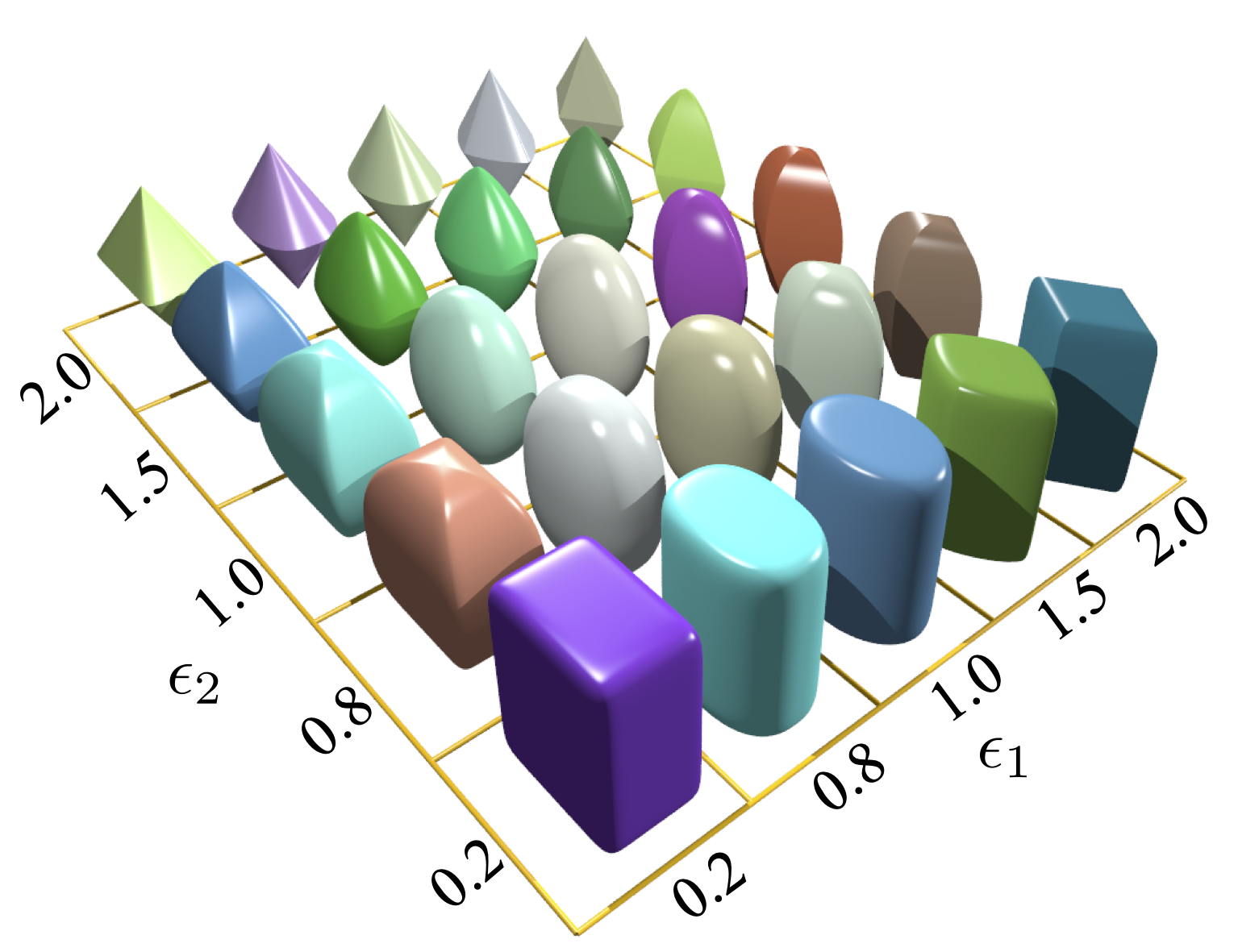
Superellipsoid.
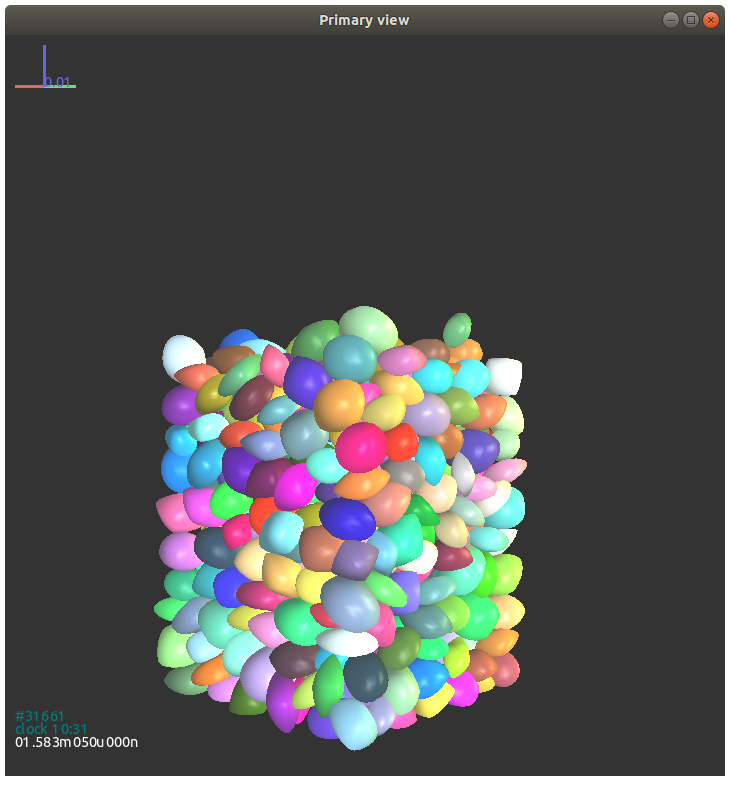
Here we give an example of a simulation of superellipsoids free falling into a cubic box.
|
|
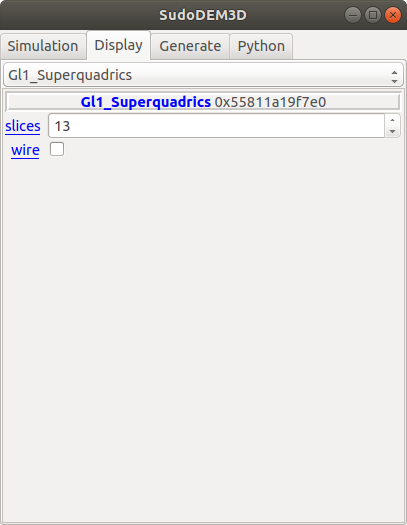
With a GUI controller, we can click ‘show 3D’ button at the panel ‘Simulation’ to display the simulating scene. On the ‘Display’ panel, select the render ‘Gl1_Superquadrics’ to configure the resolution of solid or wireframe particles, as shown in Fig. 3.3{reference-type=“ref” reference=“figguidisplay”}.
Figs. 3.4{reference-type=“ref” reference=“figexp11”} - 3.6{reference-type=“ref” reference=“figexp13”} show simulations of packing of superellipsoids at different states for the presented example.


Several properties and methods for a shape Superquadrics are listed below:
-
Properties:
-
$r_x$, $r_y$, $r_z$: float, semi-major axis lengths in x, y, and z axies.
-
$\epsilon_1$, $\epsilon_2$: float, shape parameters.
-
isSphere: bool, particle is spherical or not.
-
-
Methods:
-
getVolume(): float, return particle’s volume.
-
getrxyz(): Vector3, return particle’s rxyz.
-
geteps(): Vector2, return particle’s eps1 and eps2.
-
Here is an example to get the volume of a particle with an id of 100:
volume = O.bodies[100].shape.getVolume()
A general method to list all properties of an object is as follows:
O.bodies[100].dict()
The output is like follows:
{'bound': <Aabb instance at 0x56072ec83da0>,
'chain': -1,
'clumpId': -1,
'flags': 3,
'groupMask': 1,
'id': 100,
'iterBorn': 0,
'material': <SuperquadricsMat instance at 0x56072e6ed5f0>,
'shape': <Superquadrics instance at 0x56072ec83b60>,
'state': <State instance at 0x56072ec839e0>,
'timeBorn': 0.0}
We can see that the properties are printed in a dict form. Note that the value enclosed by pointy brackets is another object (actually, instance of an object with a specified memory address), which means that we can further access it using the ".dict()" method. Again, the properties of the object State can be accessed by:
O.bodies[100].state.dict()
The output is as follows:
{'angMom': Vector3(0,0,0),
'angVel': Vector3(0,0,0),
'blockedDOFs': 0,
'densityScaling': 1.0,
'inertia': Vector3(0.0045389863901528615,0.007287422614611933,
0.0067053718092146865),
'isDamped': True,
'mass': 3.225715855242557,
'refOri': Quaternion((1,0,0),0),
'refPos': Vector3(0,0,0),
'se3': (Vector3(0,0.8,3),
Quaternion((0.3970010520699211,0.5339678220536823,
-0.7465042060609055),2.1754719537556495)),
'vel': Vector3(0,0,0)}
For an object Shape, we list all properties which may vary for different child classes.
O.bodies[100].shape.dict()
The output is as follows:
{'color': Vector3(0.6407663308273844,0.07426042997942327,
0.05872324344642611),
'eps': Vector2(1.3975848801318045,1.5376309088540607),
'eps1': 1.3975848801318045,
'eps2': 1.5376309088540607,
'highlight': False,
'isSphere': False,
'rx': 0.1,
'rxyz': Vector3(0.1,0.06469580193313924,0.07572423080016706),
'ry': 0.06469580193313924,
'rz': 0.07572423080016706,
'wire': False}
Here we give an example to list ids and positions of all superellipsoids:
for b in O.bodies: # loop all bodies in the simulation
# we have to check if the present body is a superellipsoid or others, e.g., a wall
if isinstance(b.shape, Superquadrics): # if it is a superellipsoid, then to do
pid = b.id # get the id of particle b
pos = b.state.pos # get the position of particle b
print pid, pos