Example 3: packing of GJKparticles

Here’s where your user finds out if your project is for them.

There are five kinds of shapes, namely sphere, polyhedron, cone, cylinder and cuboid, in SudoDEM, for which the GJK algorithm of contact detection is performed [^5], so that we coined a name GJKparticle for grouping these particle shapes. In the Python module _gjkparticle_utils (see Sec. 5.1.3{reference-type=“ref” reference=“modgjkparticle”}), several construction functions are provided including:

GJKSphere(radius,margin,mat)
GJKPolyhedron(vertices,extent,margin,mat, rotate)
GJKCone(radius, height, margin, mat, rotate)
GJKCylinder(radius, height, margin, mat, rotate)
GJKCuboid(extent, margin,mat, rotate)

Note: a margin is used to expand a particle for achieving a better computational efficiency, which however should be large enough for ensuring that collision occurs in this small region but small enough for shape fidelity.

Similar to Example 1, we conduct some simulations of particles free falling into a cubic box. We first import some modules:

1
2
3
4
5
6


from sudodem import plot, _gjkparticle_utils
from sudodem import *

from sudodem._gjkparticle_utils import *
import random as rand
import math

Next, define some constants:

1
2
3
4
5
6
7
8
9


cube_v0 = [[0,0,0],[1,0,0],[1,1,0],[0,1,0],[0,0,1],[1,0,1],[1,1,1],[0,1,1]]
cube_v = [[i*0.01 for i in j] for j in cube_v0]

isSphere=False

num_x = 5
num_y = 5
num_z = 20
R = 0.01

Define a lattice grid:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


#R: distance between two neighboring nodes
#num_x: number of nodes along x axis
#num_y: number of nodes along y axis
#num_z: number of nodes along z axis
#return a list of the postions of all nodes
def GridInitial(R,num_x=10,num_y=10,num_z=20):
   pos = list()
   for i in range(num_x):
      for j in range(num_y):
         for k in range(num_z):
            x = i*R*2.0
            y = j*R*2.0
            z = k*R*2.0
            pos.append([x,y,z])       
   return pos

Set properties of materials:

1
2
3
4
5
6
7
8


p_mat = GJKParticleMat(label="mat1",Kn=1e4,Ks=7e3,frictionAngle=math.atan(0.5),density=2650,betan=0,betas=0) #define Material with default values
#mat = GJKParticleMat(label="mat1",Kn=1e6,Ks=1e5,frictionAngle=0.5,density=2650) #define Material with default values
wall_mat = GJKParticleMat(label="wallmat",Kn=1e4,Ks=7e3,frictionAngle=0.0,betan=0,betas=0) #define Material with default values
wallmat_b = GJKParticleMat(label="wallmat",Kn=1e4,Ks=7e3,frictionAngle=math.atan(1),betan=0,betas=0) #define Material with default values

O.materials.append(p_mat)
O.materials.append(wall_mat)
O.materials.append(wallmat_b)

Create the cubic box:

1
2
3
4
5
6


# create the box and add it to O.bodies
O.bodies.append(utils.wall(-R,axis=0,sense=1, material = wall_mat))#left wall along x axis
O.bodies.append(utils.wall(2.0*R*num_x-R,axis=0,sense=-1, material = wall_mat))#right wall along x axis
O.bodies.append(utils.wall(-R,axis=1,sense=1, material = wall_mat))#front wall along y axis
O.bodies.append(utils.wall(2.0*R*num_y-R,axis=1,sense=-1, material = wall_mat))#back wall along y axis
O.bodies.append(utils.wall(-R,axis=2,sense=1, material =wallmat_b))#bottom wall along z axis

Define engines and set a fixed time step:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


newton=NewtonIntegrator(damping = 0.3,gravity=(0.,0.,-9.8),label="newton",isSuperquadrics=4)

O.engines=[
   ForceResetter(),
   InsertionSortCollider([Bo1_GJKParticle_Aabb(),Bo1_Wall_Aabb()],verletDist=0.2*0.01),
   InteractionLoop(
      [Ig2_Wall_GJKParticle_GJKParticleGeom(), Ig2_GJKParticle_GJKParticle_GJKParticleGeom()], 
      [Ip2_GJKParticleMat_GJKParticleMat_GJKParticlePhys()], # collision "physics"
      [GJKParticleLaw()]   # contact law -- apply forces
   ),
   newton
]
O.dt=1e-5

Polyhedral particles are generated as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


#generate a sample
def GenSample(r,pos):
   for p in pos:
        body = GJKPolyhedron([],[1.e-2,1.e-2,1.e-2],0.05*1e-2,p_mat,False)
        body.state.pos=p
        O.bodies.append(body)   
        O.bodies[-1].shape.color=(rand.random(), rand.random(), rand.random())
        
# create a lattice grid
pos = GridInitial(R,num_x=num_x,num_y=num_y,num_z=num_z) # get positions of all nodes
# create particles at each nodes
GenSample(R,pos) #

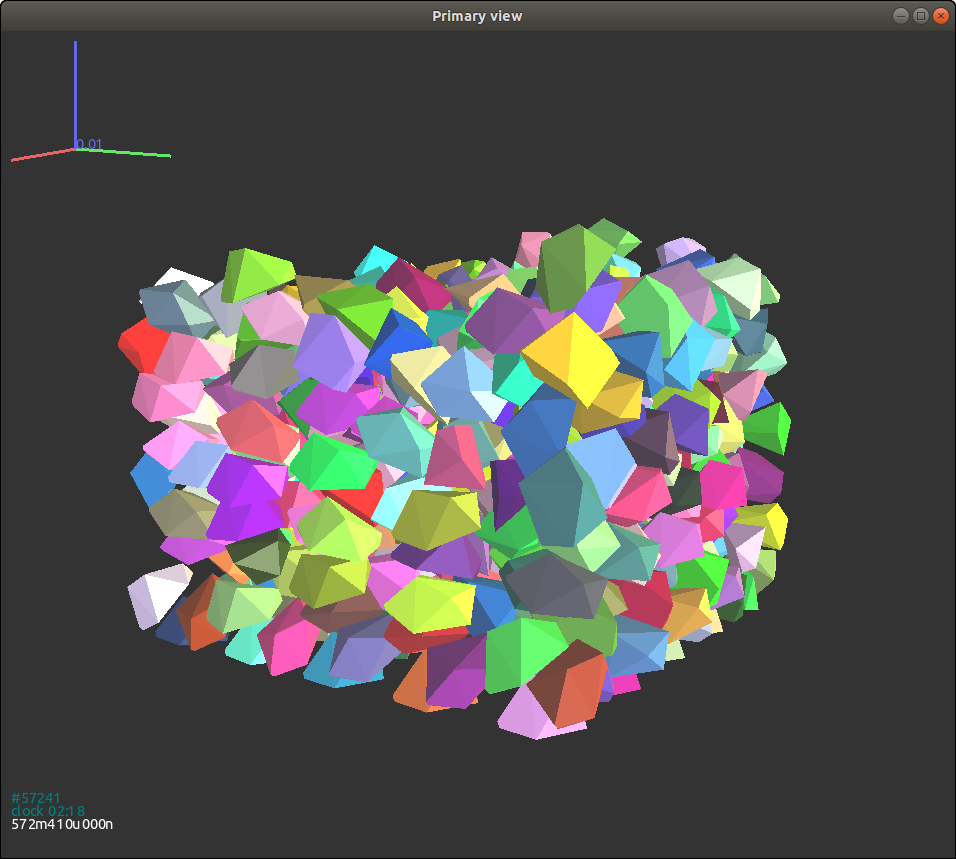Final packing of polyhedrons without random initial orientations (the
box not shown). {#figgjkpolyhedron width=“8cm”}

Final packing of cones without random initial orientations (the box
not shown). {#figgjkcone width=“8cm”}

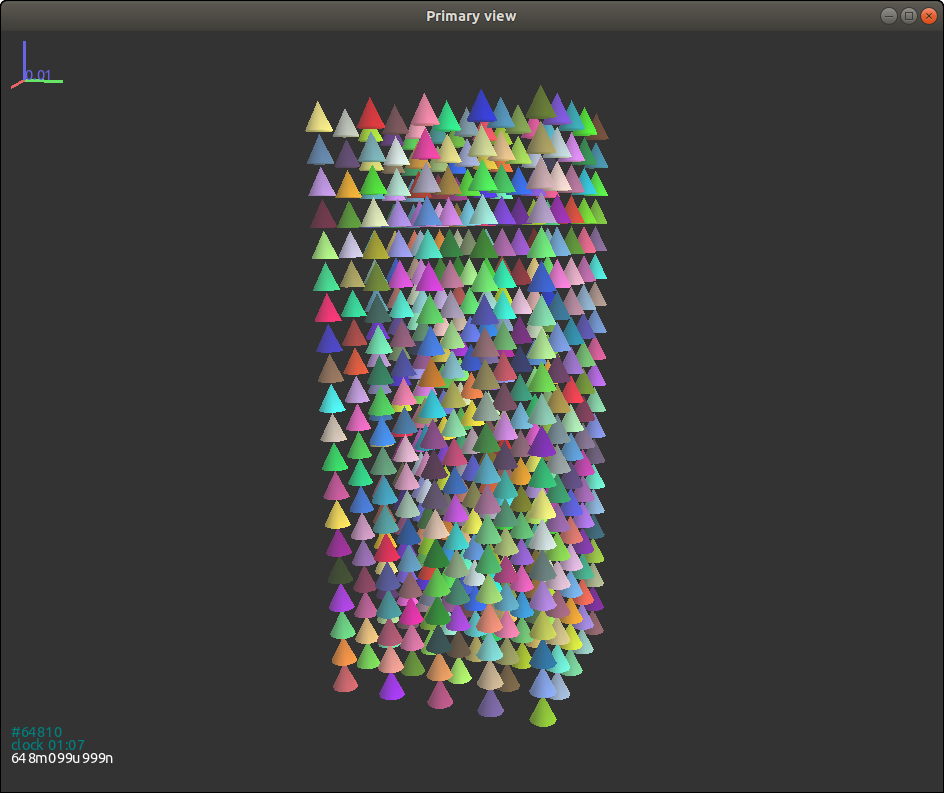
For cones, we change the GenSample functions as follows:

1
2
3
4
5
6
7


#generate a sample
def GenSample(r,pos):
   for p in pos:
        body = GJKCone(0.005,0.01,0.05*1e-2,p_mat, False)
        body.state.pos=p
        O.bodies.append(body)   
        O.bodies[-1].shape.color=(rand.random(), rand.random(), rand.random())

Fig. 3.12{reference-type=“ref” reference=“figgjkcone”} shows final packing of cones without random initial orientations (i.e., the argument rotate is False). It can be seen that particles still align in the lattice grid due to no disturbance in the tangential direction.

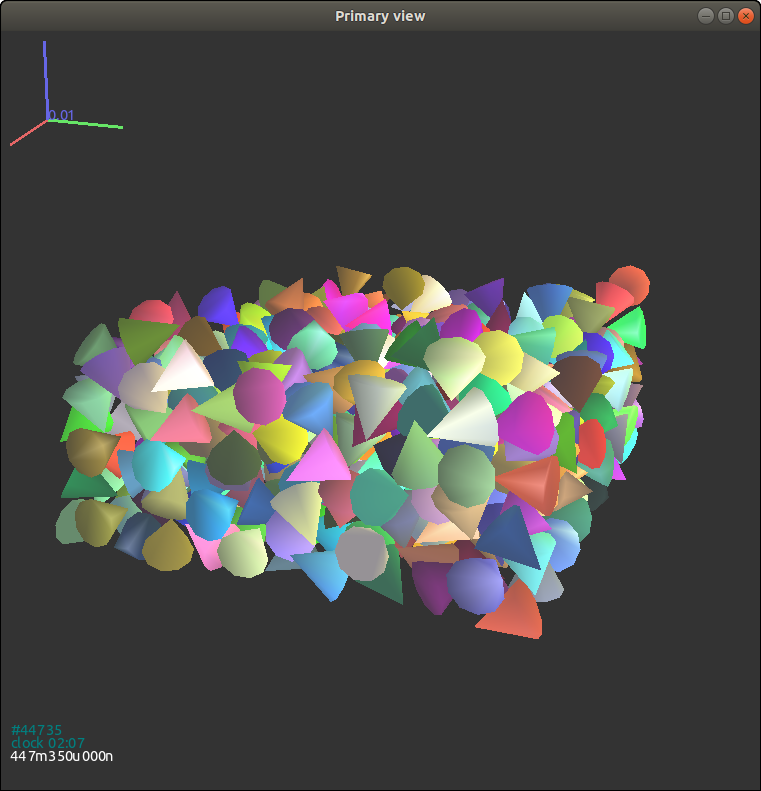
Set the argument rotate to True as follows:

1

body = GJKCone(0.005,0.01,0.05*1e-2,p_mat,True)

Final packing of cones with random initial orientations (the box not
shown). {#figgjkcone2 width=“8cm”}

Rerun the simulation, and the initial particles have random orientations. After free falling under gravity, it can be seen that the lattice alignment corrupts, referring to Fig. 3.13{reference-type=“ref” reference=“figgjkcone2”}

Final packing of cylinders without random initial orientations (the
box not shown). {#figgjkcylinder width=“8cm”}

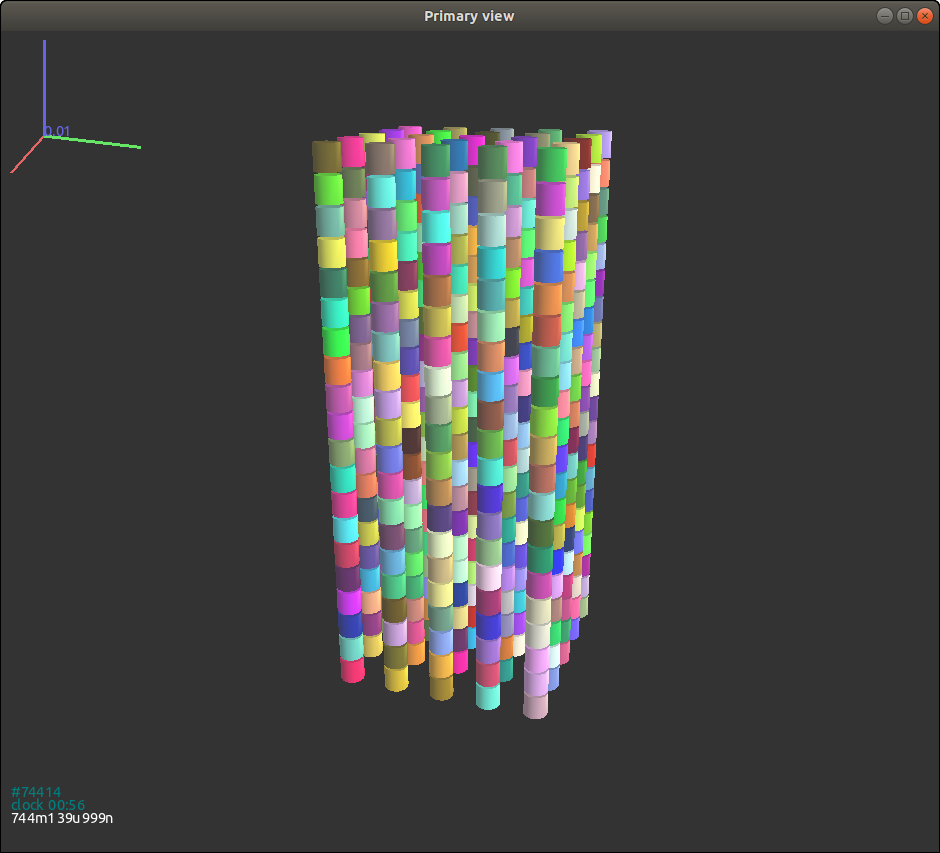
For cylindrical particles, the function GenSample is replaced as follows:

1
2
3
4
5
6


def GenSample(r,pos):
   for p in pos:
        body = GJKCylinder(0.005,0.01,0.05*1e-2,p_mat,False)
        body.state.pos=p
        O.bodies.append(body)   
        O.bodies[-1].shape.color=(rand.random(), rand.random(), rand.random())

Final packing of cylinders with random initial orientations (the box
not shown). {#figgjkcylinder2 width=“8cm”}

Rerun the simulation, we obtain final packing of cylindrical particles as shown in Fig. 3.14{reference-type=“ref” reference=“figgjkcylinder”}, where it is evident that all particles stay in a lattice grid after free falling. Again, we reset the argument rotate to True so that all initial particles will have random orientations.

1

body = GJKCylinder(0.005,0.01,0.05*1e-2,p_mat,True)

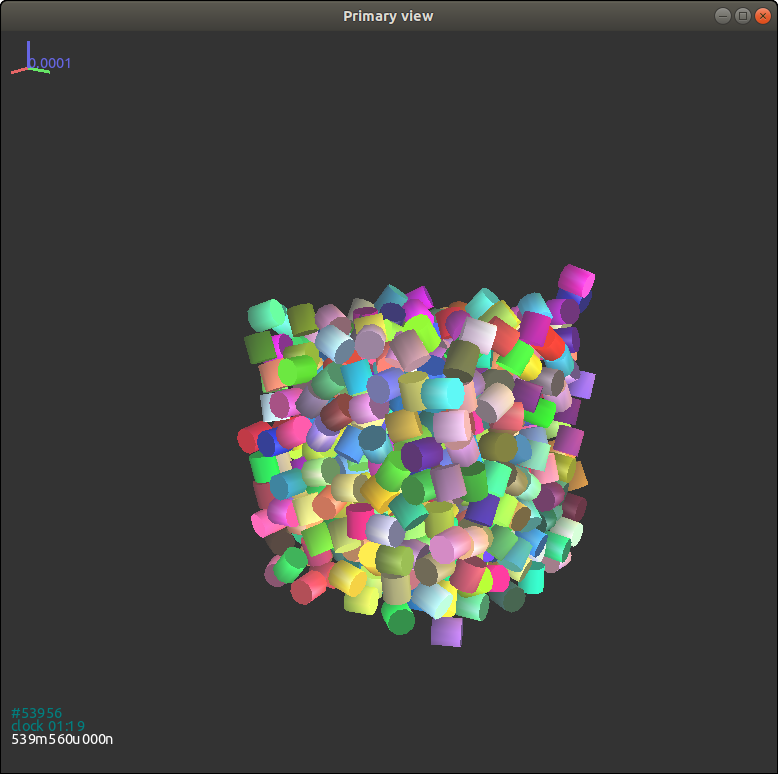
Rerun the simulation again, the column of cylindrical particles collapse into the cubic box. The final state is visualized in Fig. 3.15{reference-type=“ref” reference=“figgjkcylinder2”}.

Final packing of cuboids without random initial orientations (the box
not shown). {#figgjkcuboid width=“8cm”}

Final packing of cuboids with random initial orientations (the box not
shown). {#figgjkcuboid2 width=“8cm”}

We then continue two more simulations of cuboids. Change the function GenSample as follows:

1
2
3
4
5
6
7


#generate a sample
def GenSample(r,pos):
   for p in pos:
        body = GJKCuboid([0.005,0.005,0.005],0.05*1e-2,p_mat,False)
        body.state.pos=p
        O.bodies.append(body)   
        O.bodies[-1].shape.color=(rand.random(), rand.random(), rand.random())

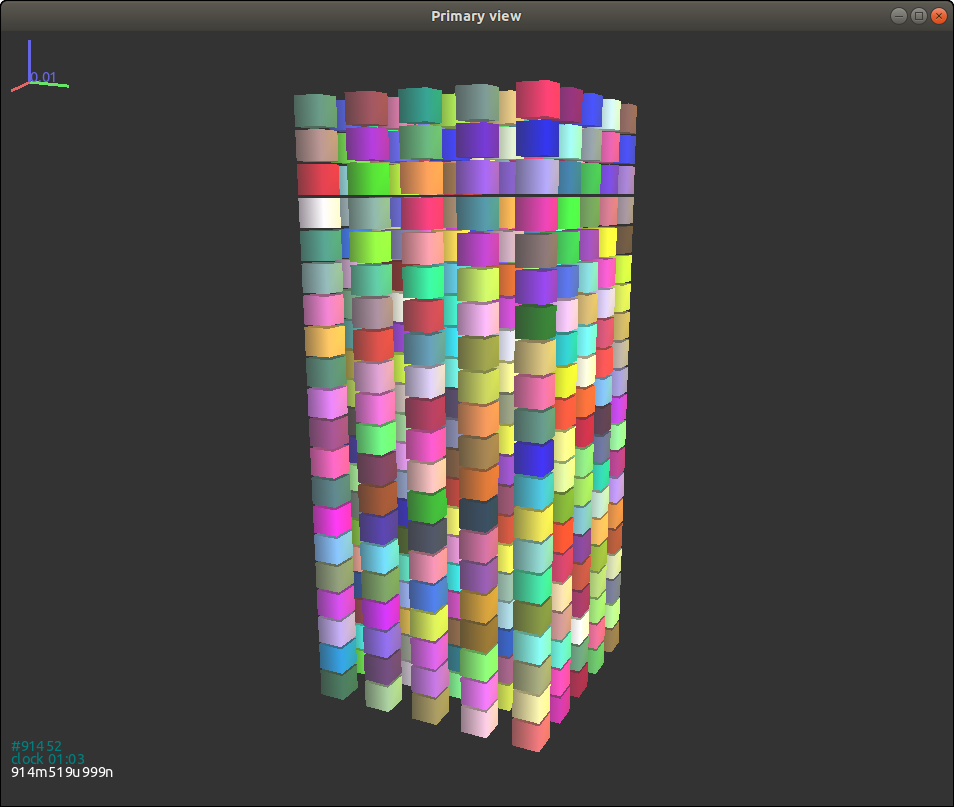
We obtain the final packing of cuboids without initial random orientations as shown in Fig. 3.16{reference-type=“ref” reference=“figgjkcuboid”}. Again, the alignment of particles remains a lattice form. Rerun the simulation with the argument rotate setting to True as follows:

1

body = GJKCuboid([0.005,0.005,0.005],0.05*1e-2,p_mat,True)

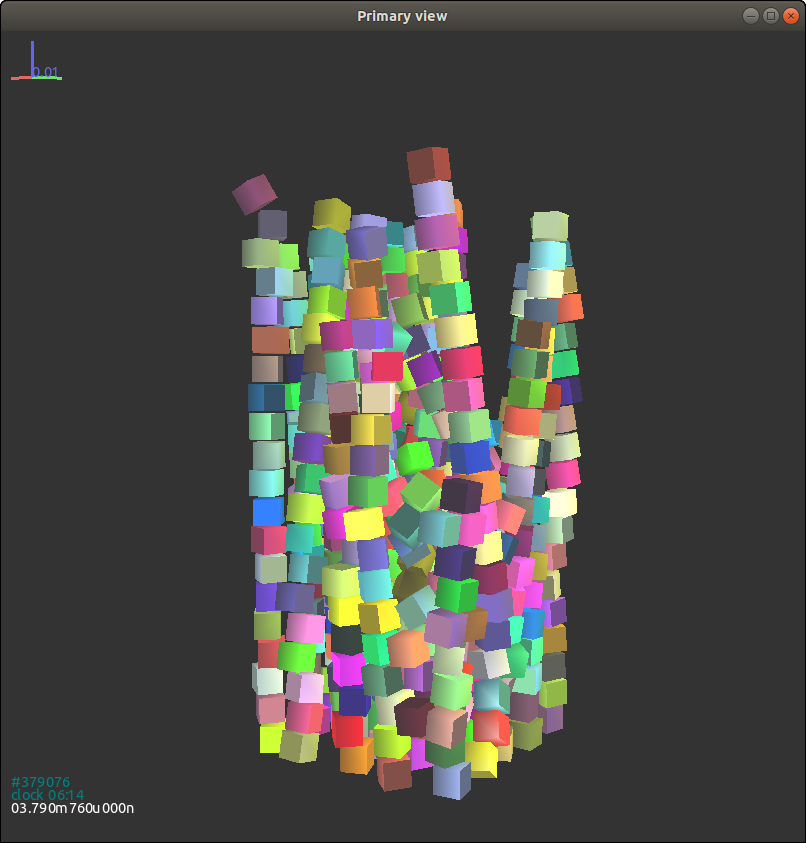
The column of particles collapses but not too much due to small gaps between particles.