这是本节的多页打印视图。 点击此处打印.

返回本页常规视图.

示例

我们给出了六个例子以期可以帮助新用户开始 SudoDEM 的学习。

我们希望如下的几个例子可以帮助用户迅速开始 SudoDEM 的学习, 例子对应的脚本可从以下 github 仓库下载:

下载地址一: 地址一 下载地址二: 地址二

1 - 示例 0: 运行一个简单的模拟

该示例模拟了一个自由落体的球体掉在地面的过程

该例子对应的 Python 脚本名字为: ‘example0.py’, 你可以选择把该例子的工作路径设置为 (例如, /home/xxx/example')。

打开命令行并键入 ‘sudodem3d example0.py’ 来运行该例子。如果当前命令行路径不在例子工作路径下，你可能需要输入相对路径来指向正确的例子所处文件夹。

‘example0.py’ 例子脚本如下:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

# 球体在重力作用下自由落体到地面

from sudodem import utils # module utils has some auxiliary functions

#1. 定义球体的材料
mat = RolFrictMat(label="mat1",Kn=1e8,Ks=7e7,frictionAngle=math.atan(0.0),density=2650) # material 1 for particles
wallmat1 = RolFrictMat(label="wallmat1",Kn=1e8,Ks=0,frictionAngle=0.) # material 2 for walls

# 将新定义的材料添加到模拟的材料数值中
# O 可被认为是当前模拟的核心类
# 可以看到材料是 O 的一个属性, 所以我们可以用点操作来获取到对应的材料对象。
O.materials.append(mat) # materials is a list, i.e., a container for all materials involving in the simulations
O.materials.append(wallmat1)
# 在将材料添加到材料数组后我们可以通过材料的标签来获取其信息。参见下面墙体的材料定义。

#　创建球体
sp = sphere((0,0,10.0),1.0, material = mat)
O.bodies.append(sp)
# 用无限大墙体来模拟地面
ground = utils.wall(0,axis=2,sense=1, material = 'wallmat1') # utils.wall defines a wall with normal parallel to one axis of the global Cartesian coordinate system. The first argument (here = 0) specifies the location of the wall, and with the keyword axis (here = 2, axis has a value of 0, 1, 2 for x, y, z axies respectively) we know that the normal of the wall is along z axis with centering at z = 0 (0, specified by the first argument); the second keyword sense (here = 1, sense can be -1, 0, 1 for negative, both, and positive sides respectively) specifies that the positive side (i.e., the normal points to the positive direction of the axis) of the wall is activated, at which we will compute the interaction of a particle and this wall; the last keyword materials specifies a material to this wall, and we assign a string (i.e., the label of wallmat1) to the keyword, and directly assigning the object of the material (i.e., wallmat1 returned by RolFrictMat) is also acceptable.
O.bodies.append(ground) # add the ground to the body container

	
# 使用PyRunner来周期性地执行函数。
def record_data():
    #open a file
    fout = open('data.dat','a') #create/open a file named 'data.dat' in append mode
    #we want to record the position of the sphere
    p = O.bodies[0] # the sphere has been appended into the list O.bodies, and we can use the corresponding index to access it. We have added two bodies in total to O.bodies, and the sphere is the first one, i.e., the index is 0.
    # p is the object of the sphere
    # as a body object, p has several properties, e.g., state, material, which can be listed by p.dict() in the commandline.
    pos = p.state.pos # get the position of the sphere
    print>>fout, O.iter, pos[0], pos[1], pos[2] # we print the iteration number and the position (x,y,z) into the file fout.
    # then, close the file and release resource
    fout.close()

# 创建牛顿引擎来使得球体的运动遵循牛顿定律
newton=NewtonIntegrator(damping = 0.1,gravity=(0.,0.0,-9.8),label="newton")
# 设置局部阻尼为 0.1, 同时设置重力加速度为 9.8 m/s2，方向为z轴朝下。

# 引擎数组是整个模拟的最核心的部分
# 在每个时步内，引擎依次运行来完成 DEM 一个完整的计算循环
O.engines=[
   ForceResetter(), # first, we need to reset the force container to store upcoming contact forces
   # next, we conduct the broad phase of contact detection by comparing axis-aligned bounding boxs (AABBs) to rule out those pairs that are definitely not contacting.
   InsertionSortCollider([Bo1_Sphere_Aabb(),Bo1_Wall_Aabb()],verletDist=0.2*0.01),
   # then, we execute the narrow phase of contact detection
   InteractionLoop( # we will loop all potentially contacting pairs of particles
	  [Ig2_Sphere_Sphere_ScGeom(), Ig2_Wall_Sphere_ScGeom()], # for different particle shapes, we will call the corresponding functions to compute the contact geometry, for example, Ig2_Sphere_Sphere_ScGeom() is used to compute the contact geometry of a sphere-sphere pair.
	  [Ip2_RolFrictMat_RolFrictMat_RolFrictPhys()], # we will compute the physical properties of contact, e.g., contact stiffness and coefficient of friction, according to the physical properties of contacting particles.
	  [RollingResistanceLaw(use_rolling_resistance=False)]   # Next, we compute contact forces in terms of the contact law with the info (contact geometric and physical properties) computed at last two steps.
   ),
   newton, # finally, we compute acceleration and velocity of each particle and update their positions.
   #at each time step, we have a PyRunner function help to hack into a DEM cycle and do whatever you want, e.g., changing particles' states, and saving some data, or just stopping the program after a certain running time. 
   PyRunner(command='record_data()',iterPeriod=10000,label='record',dead = False)
]

# 设置时步
O.dt = 1e-5

# 清空 data.dat 并写入文件头部信息
fout = open('data.dat','w') # we open the file in a write mode so that the file will be clean
print>>fout, 'iter, x, y, z' # write a file head
fout.close() # close the file

# 用户可通过如下两种方式来运行该模拟
# 1. 执行命令
# O.run()
# 或者设置时步来运行
O.run(1600000)
# 2. 在 GUI 界面点击运行按钮来运行

在命令行中键入以下命令来运行脚本

sudodem3d example0.py

多线程运行（例如, 使用2个线程 [^4])

sudodem3d -j2 example0.py

运行时所保存的数据如下所示:

iter, x, y, z
10000 0.0 0.0 9.95588676912
20000 0.0 0.0 9.82357353912
30000 0.0 0.0 9.60306030912
40000 0.0 0.0 9.29434707912
50000 0.0 0.0 8.89743384912
60000 0.0 0.0 8.41232061912
70000 0.0 0.0 7.83900738912

用户可以使用 gnuplot 来快速可视化模拟结果 (gnuplot 可通过在命令行键入以下命令来完成安装):

sudo apt install gnuplot

下图所示了 gnuplot 可视化的计算结果 3.1{reference-type=“ref” reference=“figsinglesp”}:

$> gnuplot
    gnuplot> plot 'data.dat' using ($1/10000):4; set xlabel 'iterations [x10000]'; set ylabel 'position z [m]'

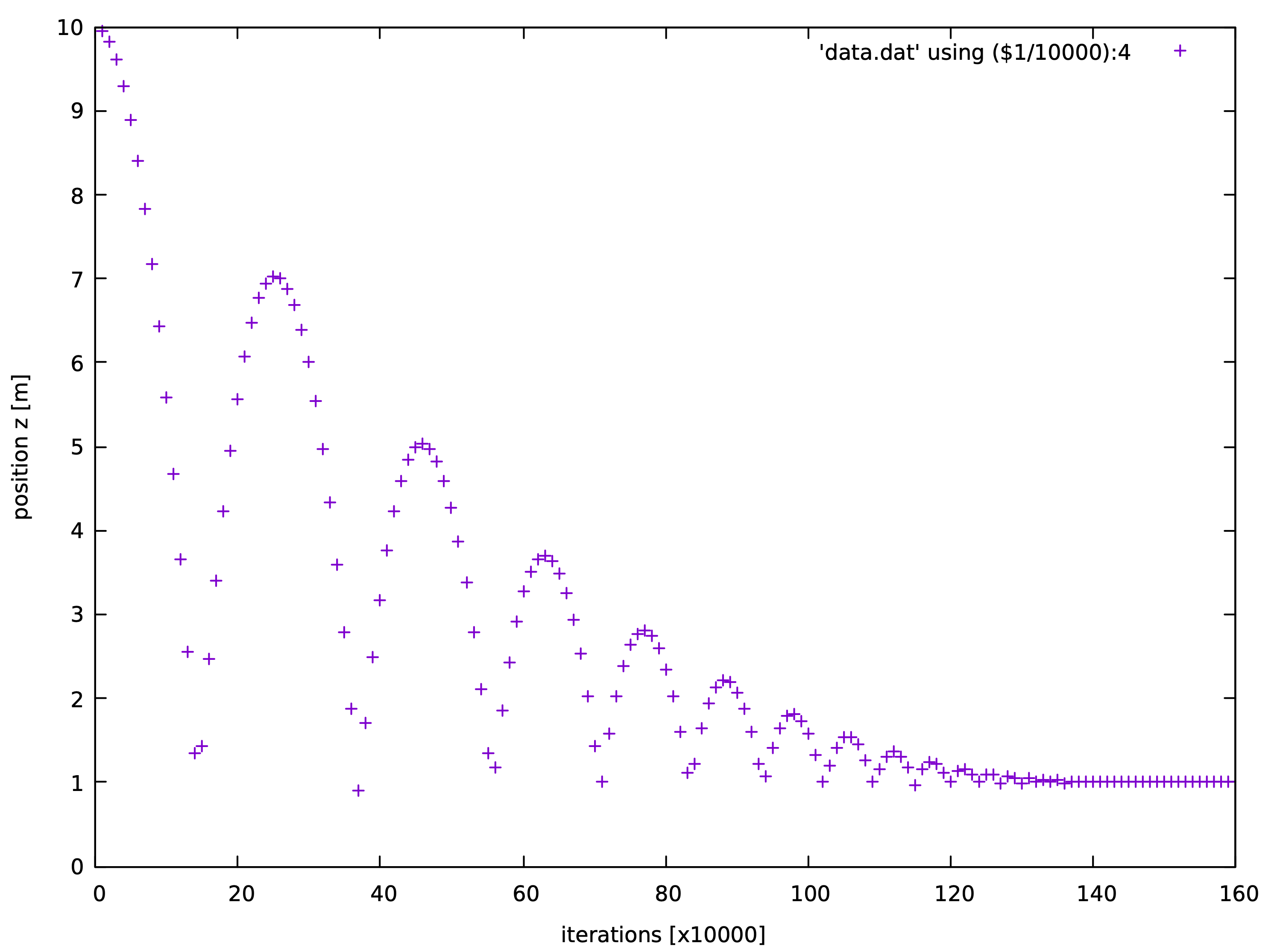
alt text

球体自由落体到地面的z方向坐标变化。

2 - 示例 1: 超级椭球堆积模拟

该示例给出了超级椭球的堆积模拟

超级椭球局部坐标下的形状函数可由下式给出 $$\label{eqsurface} \Big(\big|\frac{x}{r_x}\big|^{\frac{2}{\epsilon_1}} + \big|\frac{y}{r_y}\big|^{\frac{2}{\epsilon_1}}\Big)^{\frac{\epsilon_1}{\epsilon_2}} + \big|\frac{z}{r_z}\big|^{\frac{2}{\epsilon_2}} = 1$$ 其中 $r_x, r_y$ 和 $r_z$ 是超级椭球在x, y, z轴的半长主轴; and $\epsilon_i (i=1,2)$ 是刻画颗粒棱角度的形状参数. $\epsilon_i$ 在 0 到 2 的变化可勾勒出非常丰富的凸超级椭球形状。SudoDEM 生成超级椭球的两个函数可参见如下高亮描述 (see Sec. 5.1.2{reference-type=“ref” reference=“modsuperquadrics”}):

  • NewSuperquadrics2($r_x$, $r_y$, $r_z$, $\epsilon_1$, $\epsilon_2$, mat, rotate, isSphere)

  • NewSuperquadrics_rot2($r_x$, $r_y$, $r_z$, $\epsilon_1$, $\epsilon_2$, mat, $q_w$, $q_x$, $q_y$, $q_z$, isSphere)

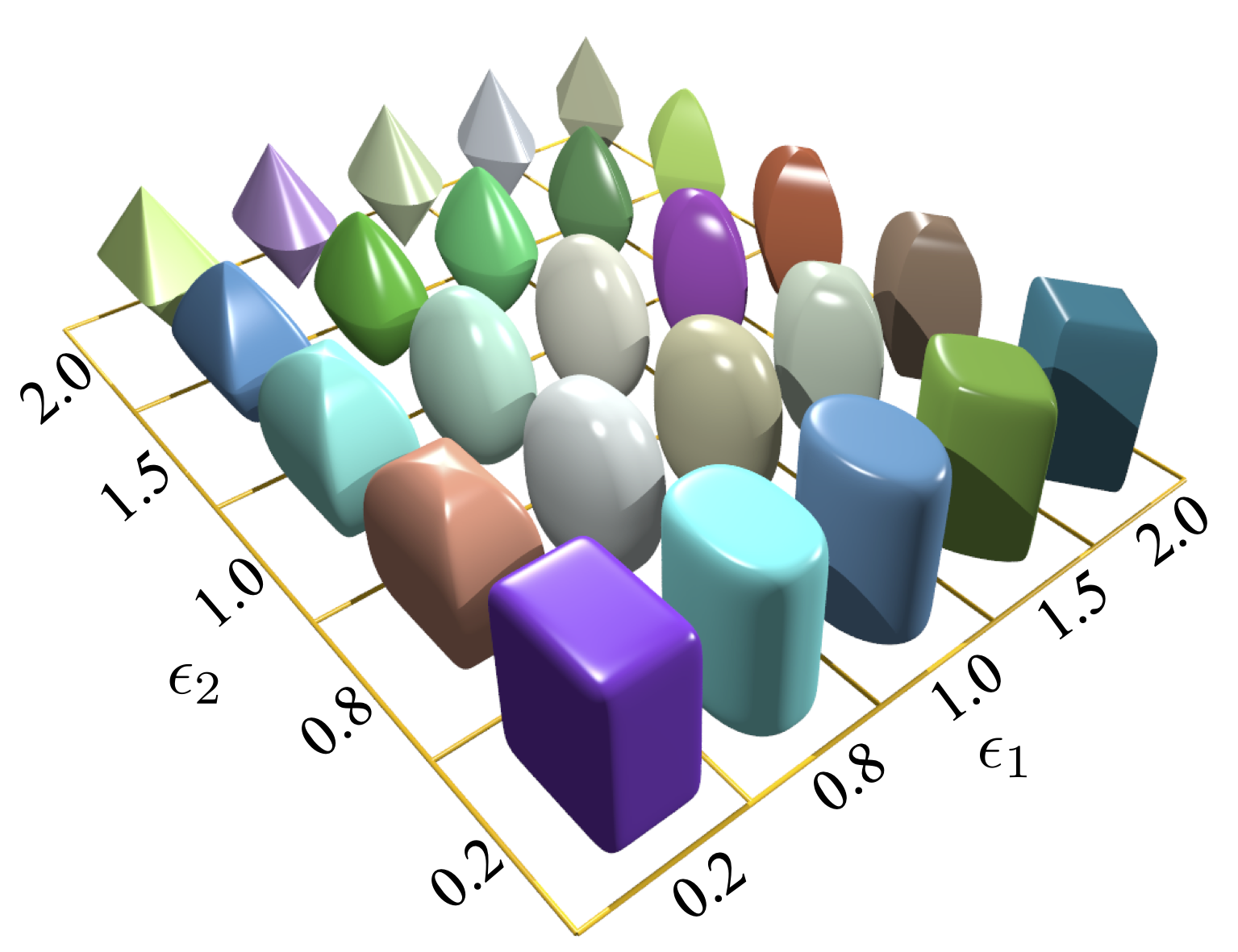
Superellipsoids.

超级椭球。

这里我们给出了超级椭球在立方体盒子中重力堆积的模拟示例。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91

###############################################
# 在栅格中生成超级椭球，随后在重力作用下堆积在立方体中
###############################################
# 导入一些必要的库
from sudodem import _superquadrics_utils

from sudodem._superquadrics_utils import *
import math
import random as rand
import numpy as np

######## 定义形状参数 #################
isSphere=False

num_x = 5
num_y = 5
num_z = 20
R = 0.1

####### 定义一些辅助函数 #########
               
# 定义栅格
# R: 两个邻近节点的距离
# num_x: x轴节点数量
# num_y: y轴节点数量
# num_z: z轴节点数量
# 返回所有节点坐标的列表
def GridInitial(R,num_x=10,num_y=10,num_z=20):
   pos = list()
   for i in range(num_x):
      for j in range(num_y):
         for k in range(num_z):
            x = i*R*2.0
            y = j*R*2.0
            z = k*R*2.0
            pos.append([x,y,z])       
   return pos

# 生成试样
def GenSample(r,pos):
   for p in pos:
		epsilon1 = rand.uniform(0.7,1.6)
		epsilon2 = rand.uniform(0.7,1.6)
		a = r
		b = r*rand.uniform(0.4,0.9)#aspect ratio
		c = r*rand.uniform(0.4,0.9)
		
		body = NewSuperquadrics2(a,b,c,epsilon1,epsilon2,p_mat,True,isSphere)
		body.state.pos=p
		O.bodies.append(body)

######### 模拟设置 ####################
# 颗粒材料设置
p_mat = SuperquadricsMat(label="mat1",Kn=1e5,Ks=7e4,frictionAngle=math.atan(0.3),density=2650,betan=0,betas=0)
# betan 和 betas 对应于接触的粘性阻尼, 默认值为0，表示无粘性阻尼.
# 侧壁墙的材料设置
wall_mat = SuperquadricsMat(label="wallmat",Kn=1e6,Ks=7e5,frictionAngle=0.0,betan=0,betas=0)
# 底部墙体的材料设置
wallmat_b = SuperquadricsMat(label="wallmat",Kn=1e6,Ks=7e5,frictionAngle=math.atan(1),betan=0,betas=0)
# 将定义的材料添加到模拟材料数组中
O.materials.append(p_mat)
O.materials.append(wall_mat)
O.materials.append(wallmat_b)

# 创建墙体对象并将其添加到模拟的形状列表中
O.bodies.append(utils.wall(-R,axis=0,sense=1, material = wall_mat))#left wall along x axis
O.bodies.append(utils.wall(2.0*R*num_x-R,axis=0,sense=-1, material = wall_mat))#right wall along x axis
O.bodies.append(utils.wall(-R,axis=1,sense=1, material = wall_mat))#front wall along y axis
O.bodies.append(utils.wall(2.0*R*num_y-R,axis=1,sense=-1, material = wall_mat))#back wall along y axis
O.bodies.append(utils.wall(-R,axis=2,sense=1, material =wallmat_b))#bottom wall along z axis

# 创建栅格
pos = GridInitial(R,num_x=num_x,num_y=num_y,num_z=num_z) # get positions of all nodes
# 在每个节点创建超级椭球颗粒
GenSample(R,pos)

# 创建引擎
# 定义牛顿引擎
newton=NewtonIntegrator(damping = 0.1,gravity=(0.,0.,-9.8),label="newton",isSuperquadrics=1) # isSuperquadrics: 1 for superquadrics

O.engines=[
   ForceResetter(), InsertionSortCollider([Bo1_Superquadrics_Aabb(),Bo1_Wall_Aabb()],verletDist=0.2*0.1),
   InteractionLoop(
      [Ig2_Wall_Superquadrics_SuperquadricsGeom(),    Ig2_Superquadrics_Superquadrics_SuperquadricsGeom()], 
      [Ip2_SuperquadricsMat_SuperquadricsMat_SuperquadricsPhys()], # collision "physics"
      [SuperquadricsLaw()]   # contact law
   ),
   newton
   
]
O.dt=5e-5

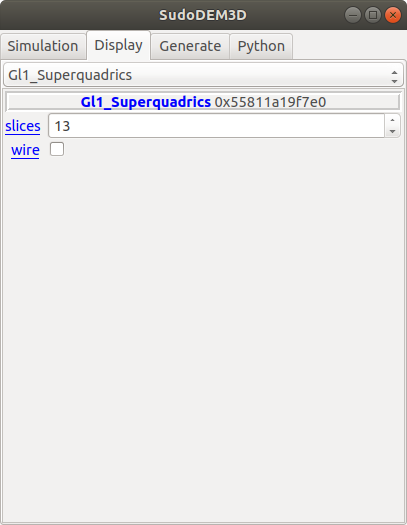
在GUI控制面板中我们可以通过点击 ‘show 3D’ 按钮来显示模拟的可视化场景。在显示模式下选择 ‘Gl1_Superquadrics’ 渲染器来控制颗粒是由线条还是由实体面来渲染（如图）， 3.3{reference-type=“ref” reference=“figguidisplay”}.

GUI for display configuration of superellipsoids.

Figs. 3.4{reference-type=“ref” reference=“figexp11”} - 3.6{reference-type=“ref” reference=“figexp13”} 显示了在不同渲染模式下的超级椭球颗粒。

Initial packing of superellipsoids.

Packing of superellipsoids during falling.

Final packing of superellipsoids.

超级椭球颗粒的属性和类方法展示如下：

  • 属性:

    • $r_x$, $r_y$, $r_z$: 浮点型, x, y, 和 z 轴的半长轴。

    • $\epsilon_1$, $\epsilon_2$: 浮点型, 材料参数。

    • isSphere: 布尔值, 颗粒是否是球体.

  • 类方法:

    • getVolume(): 浮点型, 返回颗粒体积。

    • getrxyz(): 三阶向量, 返回颗粒的三个半长轴。

    • geteps(): 二阶向量, 返回颗粒的形状参数eps1和eps2。

如下代码给出了获取索引为100的超级椭球的体积:

volume = O.bodies[100].shape.getVolume()

获取对象所有属性的方法如下:

O.bodies[100].dict()

输出如下:

{'bound': <Aabb instance at 0x56072ec83da0>,
 'chain': -1,
 'clumpId': -1,
 'flags': 3,
 'groupMask': 1,
 'id': 100,
 'iterBorn': 0,
 'material': <SuperquadricsMat instance at 0x56072e6ed5f0>,
 'shape': <Superquadrics instance at 0x56072ec83b60>,
 'state': <State instance at 0x56072ec839e0>,
 'timeBorn': 0.0}

我们可以看到对象的属性是以字典的方式被打印出来的。需要提及的是尖括号内的是另一个对象的指针，也就是说我们可以通过dict()方法来进一步获取其对应的属性。例如我们要获取颗粒state的属性，可以通过如下代码：

O.bodies[100].state.dict()

输出如下:

{'angMom': Vector3(0,0,0),
 'angVel': Vector3(0,0,0),
 'blockedDOFs': 0,
 'densityScaling': 1.0,
 'inertia': Vector3(0.0045389863901528615,0.007287422614611933,
                           0.0067053718092146865),
 'isDamped': True,
 'mass': 3.225715855242557,
 'refOri': Quaternion((1,0,0),0),
 'refPos': Vector3(0,0,0),
 'se3': (Vector3(0,0.8,3),
  Quaternion((0.3970010520699211,0.5339678220536823,
                     -0.7465042060609055),2.1754719537556495)),
 'vel': Vector3(0,0,0)}

对于 Shape对象, 它的属性输出可能随着子类的不同而不同。

O.bodies[100].shape.dict()

输出如下:

{'color': Vector3(0.6407663308273844,0.07426042997942327,
                            0.05872324344642611),
 'eps': Vector2(1.3975848801318045,1.5376309088540607),
 'eps1': 1.3975848801318045,
 'eps2': 1.5376309088540607,
 'highlight': False,
 'isSphere': False,
 'rx': 0.1,
 'rxyz': Vector3(0.1,0.06469580193313924,0.07572423080016706),
 'ry': 0.06469580193313924,
 'rz': 0.07572423080016706,
 'wire': False}

这里我们给出了一个例子用来获取所有超级椭球的序号及其位置信息:

for b in O.bodies: # loop all bodies in the simulation
    # we have to check if the present body is a superellipsoid or others, e.g., a wall
    if isinstance(b.shape, Superquadrics): # if it is a superellipsoid, then to do
        pid = b.id # get the id of particle b
        pos = b.state.pos # get the position of particle b
        print pid, pos

3 - 示例 2: 超级椭球三轴试验模拟

该示例给出了超级椭球的三轴试验模拟

该例子给出了超级椭球的三轴固结及压缩试验模拟。该模拟使用 CompressionEngine 引擎来完成, 同时用户可通过 PyRunner 引擎来自定义 CompressionEngine 引擎。固结和压缩引擎的基本设置如下:

  • 固结

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

        triax=CompressionEngine(
        goalx = 1.0e5, # 围压 100 kPa
        goaly = 1.0e5,
        goalz = 1.0e5,
        savedata_interval = 10000,
        echo_interval = 2000,
        continueFlag = False,
        max_vel = 100.0,
        gain_alpha = 0.5,
        f_threshold = 0.01, 
        fmin_threshold = 0.01, #偏应力与平均应力的比值
        unbf_tol = 0.01, #不平衡力比值
        file='record-con'
    )

    • goalx = goaly = goalz = 围压

    • savedata_interval: 保存模拟信息 (轴应变,体应变,平均应力和偏应力) 到文件的DEM时步周期，在固结引擎中该选项已被弃用。

    • echo_interval: 显示模拟信息 (时步, 不平衡力比值, 各个方向的应力) 到命令行的DEM时步周期。

    • continueFlag: 用来表示继续固结或压缩的保留关键字。

    • max_vel: 墙体最大移动速度，可在固结时用于限制墙体的移动。

    • gain_alpha $\alpha$: 用来控制墙体下一步的移动速度。 $$v_w = \alpha \frac{f_w - f_g}{\Delta t \sum k_n}$$ 其中， $v_w$ 表示墙体在下一时步的移动速度; $f_w$ 和 $f_g$ 分别表示当前和目标接触力; $\Delta t$ 表示时步; $\sum k_n$ 表示墙体和所有接触颗粒的接触刚度之和。

    • f_threshold $\alpha_f$: 归一化的接触力偏离比值, 即, $$\alpha_f = \frac{|f_w-f_g|}{f_g}$$

    • fmin_threshold $\beta_f$: 偏应力 $q$ 和平均主应力 $p$ 的比值, 即, $$\beta_f = \frac{q}{p},\quad p= \frac{\sigma_{ii}}{3},\quad q=\sqrt{\frac{3}{2}\sigma_{ij}^{'}\sigma_{ij}^{'}}$$ $$\sigma_{ij} = \frac{1}{V}\sum_{c\in V}f_i^cl_j^c,\quad \sigma_{ij}^{'}=\sigma_{ij}-p\delta_{ij}$$ 其中 $\sigma_{ij}$ 表示颗粒集合体的应力张量, $\sigma_{ij}^{'}$ 表示应力张量的偏应力部分; $V$ 表示试样体积; $f^c$ 和 $l^c$ 分别表示接触 $c$ 的接触力和接触支向量; $\delta_{ij}$ 表示克罗纳克尔。

    • unbf_tol $\gamma_f$: 表示不平衡力比值，由下式给出 　　$$\gamma_f = \frac{\sum\limits_{B_i\in V} |\sum\limits_{j\in B_i}f^c_j+f^b_j|}{2\sum\limits_{c\in V}|f^c|}$$ 需要说明的是只有当 $\alpha_f$, $\beta_f$ 和 $\gamma_f$ 都达到设定值，固结过程才会结束。

    • file: 模拟信息输出的文件相关信息

  • 压缩

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

        triax=CompressionEngine(
        z_servo = False,
        goalx = 1.0e5,
        goaly = 1.0e5,
        goalz = 0.01,
        ramp_interval = 10,
        ramp_chunks = 2,
        savedata_interval = 1000,
        echo_interval = 2000,
        max_vel = 10.0,
        gain_alpha = 0.5,
        file='sheardata',
        target_strain = 0.4,
        gain_alpha = 0.5
    )

    • z_servo: 布尔值，用来控制z方向是应变加载还是应力加载，在应变加载状态下 goalz 是对应的应变加载速率。

    • ramp_interval: 逐级加载到稳定应变速率的时步。该变量用来模拟实际试验中逐级稳定加载的过程，用户可以通过设定一个很小的值来忽略这个变量的影响。

    • ramp_chunks: 逐级加载到稳定应变速率的区间数。与 ramp_interval 类似，用户可以通过设定较小值来忽略它的影响。

    • target_strain: 加载目标应变 (对数应变)，在应变达到该值的时候剪切模拟停止。

      注: 如果用户需要进行准静态的三轴剪切模拟，剪切速率要低于一定的阈值。特别地，我们使用加载惯性系数来表征加载的准静态性， 即当惯性系数 $I$ 低于 $10^{-3}$时可视为准静态剪切，其中惯性系数由下式给出 $$I = \dot{\epsilon_1}\frac{\hat{d}}{\sqrt{\sigma_0/\rho}}$$ 其中 $\dot{\epsilon_1}=\mathrm{d}\epsilon_1/\mathrm{d}t$ 表示剪切应变加载速率; $\hat{d}$ 和 $\rho$ 分别表示颗粒的平均直径和平均密度， $\sigma_0$ 表示围压。

我们这里给出了一个三轴剪切加载的例子作为参考:

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134

##################################################
from sudodem import plot, _superquadrics_utils
from sudodem._superquadrics_utils import *

import math
import random as rand
rand.seed(11245642)
####################################################
epsilon = 1.4
isSphere = False
boxsize=[16.2e-3,16.2e-3,16.2e-3]
############################
#一些辅助函数
#生成单一粒径的超椭球颗粒，它们的初始位置和朝向是随机的
def gen_sample(width, depth, height, r_max = 1.0e-3):
   b_num_tot = 5000
   for j in range(b_num_tot):
      rb = r_max*0.5
      x = rand.uniform(rb, width-rb)
      y = rand.uniform(rb, depth - rb)
      z = rand.uniform(rb, height - rb)
      r = r_max*0.5
      b = NewSuperquadrics2(r*1.25,r,r,epsilon,epsilon,mat,True,isSphere)
      b.state.pos=(x, y, z)
      O.bodies.append(b)
#材料参数定义
mat = SuperquadricsMat(label="mat1",Kn=3e4,Ks=3e4,frictionAngle=math.atan(0.1),density=2650e4) #define Material with default values
wallmat1 = SuperquadricsMat(label="wallmat1",Kn=1e6,Ks=0.,frictionAngle=0.) #define Material with default values
wallmat2 = SuperquadricsMat(label="wallmat2",Kn=1e6,Ks=0.,frictionAngle=0.) #define Material with default values
O.materials.append(mat)
O.materials.append(wallmat1)
O.materials.append(wallmat2)
#############################################
#####生成真三轴的墙体
############################################
O.bodies.append(utils.wall(0,axis=0,sense=1, material = 'wallmat1'))#left x
O.bodies.append(utils.wall(boxsize[0],axis=0,sense=-1, material = 'wallmat1'))#right x
O.bodies.append(utils.wall(0,axis=1,sense=1, material = 'wallmat1'))#front y
O.bodies.append(utils.wall(boxsize[1],axis=1,sense=-1, material = 'wallmat1'))#back y
	
O.bodies.append(utils.wall(0,axis=2,sense=1, material = 'wallmat2'))#bottom z
O.bodies.append(utils.wall(boxsize[2],axis=2,sense=-1, material = 'wallmat2'))#top z
#####生成颗粒

gen_sample(boxsize[0], boxsize[1], boxsize[2])

####用来保存模拟数据的函数
def savedata():
        O.save(str(O.time)+'.xml.bz2')  
        
#########################################  
####三轴引擎
#注意: 压缩引擎默认前六个形状对象是墙体，所以在生成颗粒和墙体时，墙体总是要先于颗粒生成
triax=CompressionEngine(
   goalx = 1.0e5, # confining stress 100 kPa
   goaly = 1.0e5,
   goalz = 1.0e5,
	savedata_interval = 10000,
	echo_interval = 2000,
	continueFlag = False,
	max_vel = 10.0,
   gain_alpha = 0.5,
   f_threshold = 0.01, #1-f/goal
   fmin_threshold = 0.01, #the ratio of deviatoric stress to mean stress
   unbf_tol = 0.01, #unblanced force ratio
	file='record-con',
)

############################


      
newton=NewtonIntegrator(damping = 0.3,gravity=(0.,0.,0.),label="newton",isSuperquadrics=1)
O.engines=[
   ForceResetter(),
   InsertionSortCollider([Bo1_Superquadrics_Aabb(),Bo1_Wall_Aabb()],verletDist=0.1e-3),
   InteractionLoop(
      [Ig2_Wall_Superquadrics_SuperquadricsGeom(), Ig2_Superquadrics_Superquadrics_SuperquadricsGeom()], 
      [Ip2_SuperquadricsMat_SuperquadricsMat_SuperquadricsPhys()],
      [SuperquadricsLaw()]
   ),
   triax,
   newton,
   PyRunner(command='quiet_ball()',iterPeriod=2,iterLast = 50000,label='calm',dead = False),
   PyRunner(command='savedata()',realPeriod=7200.0,label='savedata',dead = False)#saving data every two hours
]


#删除在真三轴剪切盒之外的颗粒
def del_balls():
        num_del = 0
        #墙体位置
        left = O.bodies[0].state.pos[0]#x
        right = O.bodies[1].state.pos[0]
        front = O.bodies[2].state.pos[1]#y
        back = O.bodies[3].state.pos[1]
        bottom = O.bodies[4].state.pos[2]#z
        top = O.bodies[5].state.pos[2]
        for b in O.bodies:
                if isinstance(b.shape,Superquadrics):
                        (x,y,z) = b.state.pos
                        if x > right or x < left or y < front or y > back or z < bottom or z > top:
                                O.bodies.erase(b.id)
                                num_del += 1
        print str(num_del)+" particles are deleted!"           
                               


def quiet_ball():
    global calm_num
    
    newton.quiet_system_flag = True
    if calm_num > 2000:
        O.engines[-2].iterPeriod= 5
        calm_num += 5
    else:
        calm_num += 2
    if calm_num > 40000:
        if calm_num < 40010:
            print "calm procedure is over"
            del_balls()
        if calm_num > 50000:
            O.engines[-2].dead = True
            O.save("init_assembly.xml.bz2")
            #固结引擎开始
            triax.dead=False
            print "consolidation begins"
    
    
O.dt=1e-4


triax.dead=True
calm_num = 0

命令行将会有如下信息显示

calm procedure is over
0 particles are deleted!
consolidation begins
Iter 50000 Ubf 0.483161, Ss_x:9.67986e-05, Ss_y:4.15364e-05, Ss_z:6.1184e-05, e:0.992618
Iter 52000 Ubf 0.461741, Ss_x:1.2412, Ss_y:1.06812, Ss_z:1.10116, e:0.854445
Iter 54000 Ubf 0.263699, Ss_x:1.75334, Ss_y:1.98567, Ss_z:1.62181, e:0.757469
Iter 56000 Ubf 0.118329, Ss_x:3.06302, Ss_y:3.54818, Ss_z:3.22986, e:0.679106
Iter 58000 Ubf 0.0110747, Ss_x:22.0177, Ss_y:21.3303, Ss_z:21.3485, e:0.614824
Iter 60000 Ubf 0.000577066, Ss_x:91.4199, Ss_y:89.6039, Ss_z:89.1057, e:0.58984
Iter 62000 Ubf 0.000128293, Ss_x:100.012, Ss_y:99.7251, Ss_z:99.6123, e:0.587807
consolidation completed!

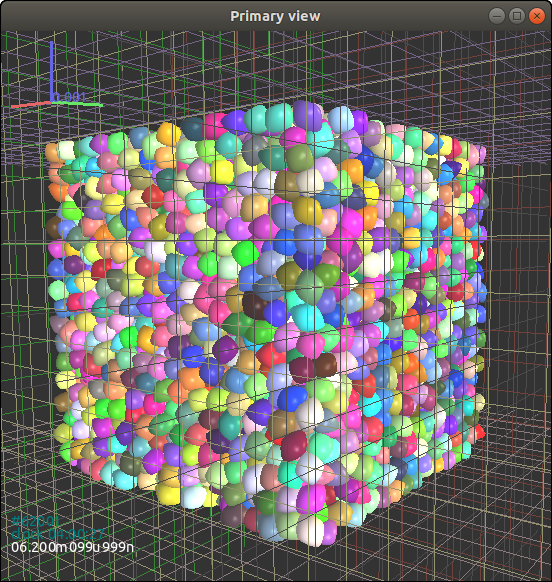
Packing of superellipsoids after consolidation.

固结完成后 (如图 Fig. [3.7] 所示，(#figex2consol){reference-type=“ref” reference=“figex2consol”}), 我们可以保存固结完成后的颗粒状态到文件中

1

O.save("final_con.xml.bz2")

然后我们开始对固结后的试样进行剪切，参见下面的脚本：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

##################################################
from sudodem import plot, _superquadrics_utils

from sudodem._superquadrics_utils import *

import math

saving_num = 0
####################################################
def savedata():
        global saving_num
        saving_num += 1
        O.save('shear'+str(saving_num)+'.xml.bz2')  
        
def quiet_system():
    for i in O.bodies:
        i.state.vel=(0.,0.,0.)
        i.state.angVel=(0.,0.,0.)
suffix=""
O.load("final_con"+suffix+".xml.bz2")
triax = O.engines[3]
O.dt = 5e-5
friction = 0.5
O.materials[0].frictionAngle=math.atan(friction)
if 1:
   for itr in O.interactions:
      id = min(itr.id1,itr.id2)
      if id > 5:
         itr.phys.tangensOfFrictionAngle = friction

#########################
#剪切开始
#########################
def shear():
    quiet_system()
    triax.z_servo = False
    triax.ramp_interval = 10
    triax.ramp_chunks = 2
    triax.file="sheardata"+suffix
    triax.goalz = 0.01
    triax.goalx = 1e5
    triax.goaly = 1e5
    triax.savedata_interval = 2500
    triax.echo_interval = 2000
    triax.target_strain = 0.4
    
shear()

O.engines[-1].iterPeriod = 2500
O.engines[-1].realPeriod = 0.0

试样的剪切加载总应变为40%，剪切终止时的试样状态如图所示 Fig. 3.8{reference-type=“ref” reference=“figex2shear”}.

Packing of superellipsoids after shear.

试样在剪切阶段的宏观力学响应可以用应力张量来表征，该张量由下式子得到: $$\label{eqDEMstress} \sigma_{ij} = \frac{1}{V} \sum_{c \in V} f_i^c l_j^c$$ 其中 $V$ 表示试样总体积； $f^c$ 表示接触 $c$ 的接触力矢量； $l^c$ 表示接触对应的支向量，也就是连接接触两颗粒质心的矢量。 平均主应力 $p$ 和偏应力 $q$ 被定义为: $$p = \frac{1}{3}\sigma_{ii},\quad q = \sqrt{\frac{3}{2} \sigma_{ij}^{'}\sigma_{ij}^{'}}$$ 其中 $\sigma_{ij}^{'}$ 表示应力张量的偏应力部分 $\sigma_{ij}$.

考虑到立方体试样的加载是由六个刚性墙来伺服控制的，轴向应变 $\epsilon_z$ 和 体应变 $\epsilon_v$ 可以由墙体的位置近似的给出, 即, $$\epsilon_z = \int_{H_0}^{H}\frac{\mathrm{d}h}{h}=-\ln\frac{H_0}{H},\quad \epsilon_v = \epsilon_x+\epsilon_y+\epsilon_z=\int_{V_0}^{V}\frac{\mathrm{d}v}{v}=-\ln\frac{V_0}{V}$$ 其中 $H$ 和 $V$ 分别表示剪切状态下的墙体高度和体积, $H_0$ 和 $V_0$ 表示刚性强初始状态的高度和体积。 体应变正值表示试样的剪胀状态。

剪切过程的数据保存格式如下：

AxialStrain VolStrain meanStress deviatorStress
0.000511000266 0.000490480823 106090.98 15931.56
0.003011001516 0.002450117535 131061.41 85718.91
0.005511002766 0.003867756447 148076.65 131980.95
0.008011004016 0.004825115794 159924.28 163706.90 
0.010511005266 0.005409561745 168606.27 186520.14
0.013011006516 0.005673777079 175131.53 203243.28
0.015511007766 0.005650846281 180293.19 216248.17
0.018011009016 0.005393122254 184581.23 227010.23

进而我们可以绘制出三轴剪切过程的应力-应变曲线以及应力路径曲线，如图所示 Figs. 3.9{reference-type=“ref” reference=“figex2shearstress”} and 3.10{reference-type=“ref” reference=“figex2shearpath”}.

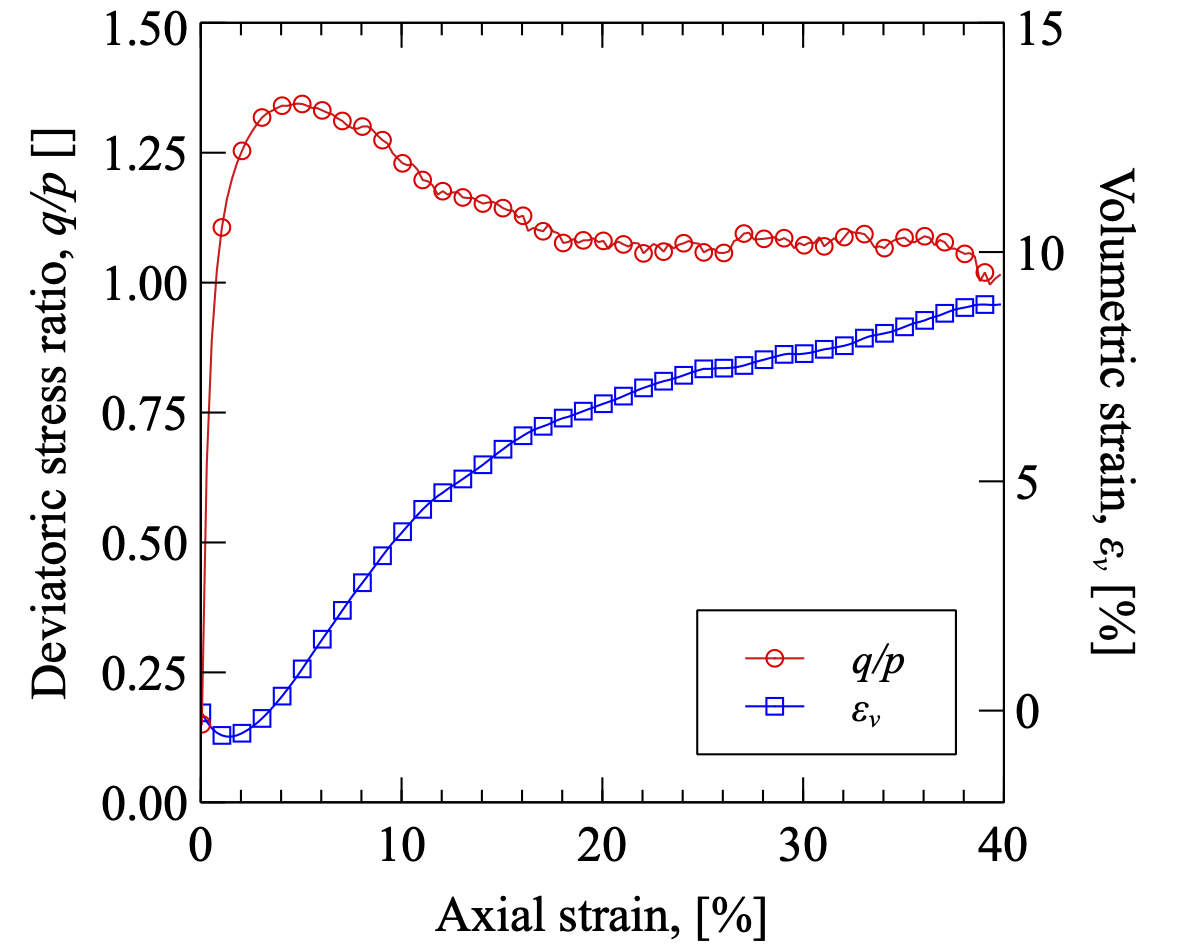
Variation of deviatoric stress ratio $q/p$ and volumetric strain $\epsilon_v$ with axial strain during shearing.

剪切过程中的应力应变曲线以及体应变曲线。

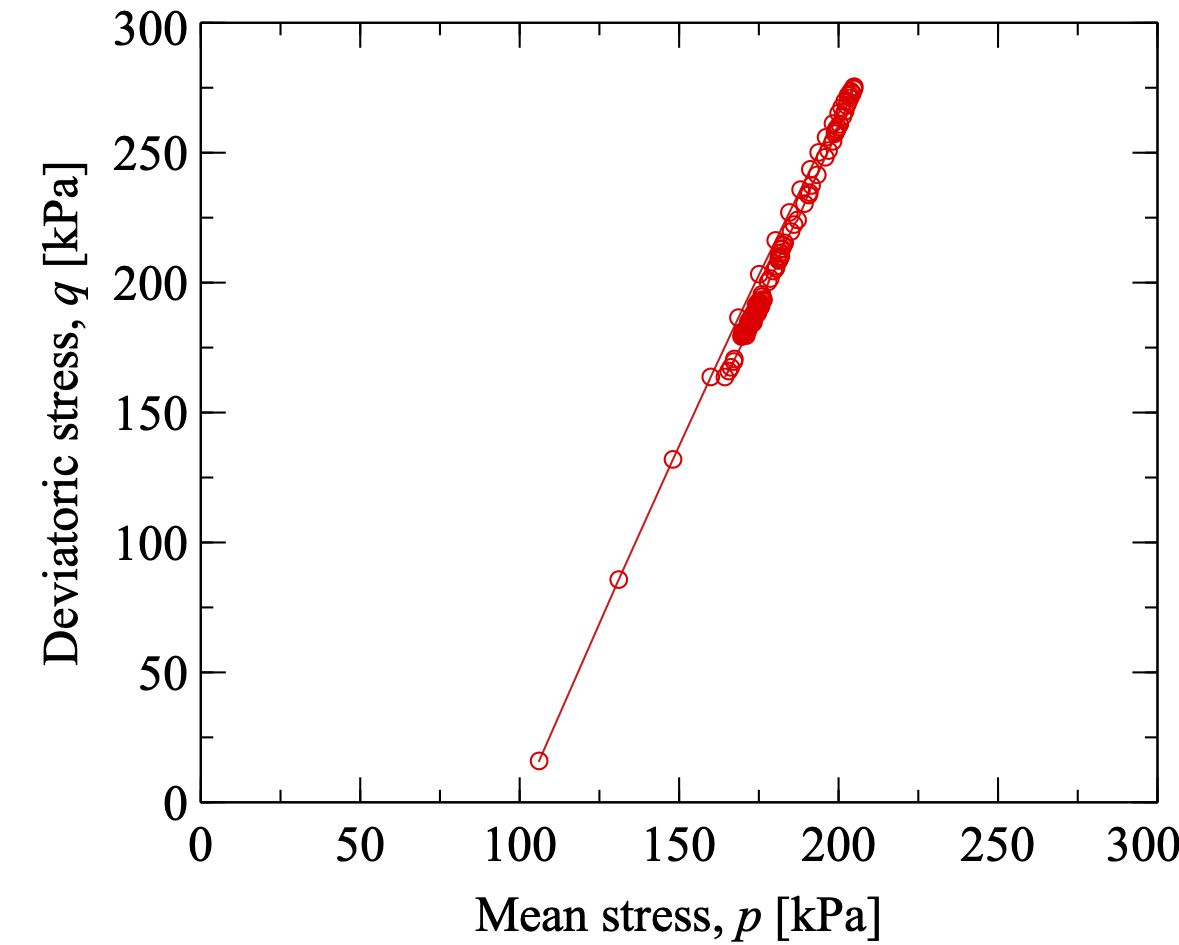
Loading path during shearing.

剪切过程中的应力路径变化。

在剪切过程中，试样状态会不断地被保存在文件中，(例如， "shearxxx.xml.bz2") 用于随后的后处理，比如我们可以利用试样加载的元数据来获得试样的配位数和组构等信息。

4 - 示例 3: GJK颗粒的堆积模拟

该示例用于GJK颗粒的堆积过程模拟

SudoDEM 中有五种颗粒它们的接触检测算法是用GJK算法实现的，即球体，多面体，圆锥体，圆柱体以及立方体[^5], 我们我们采用GJK颗粒来统一的归类如上颗粒。对应的，Python脚本中该颗粒可以用以下包来导入 _gjkparticle_utils (see Sec. 5.1.3{reference-type=“ref” reference=“modgjkparticle”}), 这五种颗粒的构造函数如下所示：

  • GJKSphere(radius,margin,mat)

  • GJKPolyhedron(vertices,extent,margin,mat, rotate)

  • GJKCone(radius, height, margin, mat, rotate)

  • GJKCylinder(radius, height, margin, mat, rotate)

  • GJKCuboid(extent, margin,mat, rotate)

注: 每个颗粒都被放大了一定的倍数用于加速颗粒接触检测算法，该放大倍数要足够大用以保证颗粒颗粒在较小尺度下可以发生接触， 同时该放大倍数要足够小，以避免颗粒形状的过度失真。

与示例1类似, 我们将会模拟GJK颗粒在立方体盒子中的自由落体堆积过程。进行模拟前，我们需要先导入如下包:

1
2
3
4
5
6

from sudodem import plot, _gjkparticle_utils
from sudodem import *

from sudodem._gjkparticle_utils import *
import random as rand
import math

定义生成颗粒的参数信息：

1
2
3
4
5
6
7
8
9

cube_v0 = [[0,0,0],[1,0,0],[1,1,0],[0,1,0],[0,0,1],[1,0,1],[1,1,1],[0,1,1]]
cube_v = [[i*0.01 for i in j] for j in cube_v0]

isSphere=False

num_x = 5
num_y = 5
num_z = 20
R = 0.01

定义颗粒生成栅格：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

#R: 相邻节点的距离
#num_x: x轴节点数量
#num_y: y轴节点数量
#num_z: z轴节点数量
#返回所有节点的位置信息
def GridInitial(R,num_x=10,num_y=10,num_z=20):
   pos = list()
   for i in range(num_x):
      for j in range(num_y):
         for k in range(num_z):
            x = i*R*2.0
            y = j*R*2.0
            z = k*R*2.0
            pos.append([x,y,z])       
   return pos

设置材料属性

1
2
3
4
5
6
7
8

p_mat = GJKParticleMat(label="mat1",Kn=1e4,Ks=7e3,frictionAngle=math.atan(0.5),density=2650,betan=0,betas=0) #define Material with default values
#mat = GJKParticleMat(label="mat1",Kn=1e6,Ks=1e5,frictionAngle=0.5,density=2650) #define Material with default values
wall_mat = GJKParticleMat(label="wallmat",Kn=1e4,Ks=7e3,frictionAngle=0.0,betan=0,betas=0) #define Material with default values
wallmat_b = GJKParticleMat(label="wallmat",Kn=1e4,Ks=7e3,frictionAngle=math.atan(1),betan=0,betas=0) #define Material with default values

O.materials.append(p_mat)
O.materials.append(wall_mat)
O.materials.append(wallmat_b)

生成立方体盒子

1
2
3
4
5
6

# create the box and add it to O.bodies
O.bodies.append(utils.wall(-R,axis=0,sense=1, material = wall_mat))#left wall along x axis
O.bodies.append(utils.wall(2.0*R*num_x-R,axis=0,sense=-1, material = wall_mat))#right wall along x axis
O.bodies.append(utils.wall(-R,axis=1,sense=1, material = wall_mat))#front wall along y axis
O.bodies.append(utils.wall(2.0*R*num_y-R,axis=1,sense=-1, material = wall_mat))#back wall along y axis
O.bodies.append(utils.wall(-R,axis=2,sense=1, material =wallmat_b))#bottom wall along z axis

生成模拟引擎并设置固定时步：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

newton=NewtonIntegrator(damping = 0.3,gravity=(0.,0.,-9.8),label="newton",isSuperquadrics=4)

O.engines=[
   ForceResetter(),
   InsertionSortCollider([Bo1_GJKParticle_Aabb(),Bo1_Wall_Aabb()],verletDist=0.2*0.01),
   InteractionLoop(
      [Ig2_Wall_GJKParticle_GJKParticleGeom(), Ig2_GJKParticle_GJKParticle_GJKParticleGeom()], 
      [Ip2_GJKParticleMat_GJKParticleMat_GJKParticlePhys()], # collision "physics"
      [GJKParticleLaw()]   # contact law -- apply forces
   ),
   newton
]
O.dt=1e-5

多面体颗粒生成如下所示：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

#生成试样
def GenSample(r,pos):
   for p in pos:
        body = GJKPolyhedron([],[1.e-2,1.e-2,1.e-2],0.05*1e-2,p_mat,False)
        body.state.pos=p
        O.bodies.append(body)   
        O.bodies[-1].shape.color=(rand.random(), rand.random(), rand.random())
        
# 生成栅格
pos = GridInitial(R,num_x=num_x,num_y=num_y,num_z=num_z) # get positions of all nodes
# 为每个节点生成颗粒
GenSample(R,pos) #

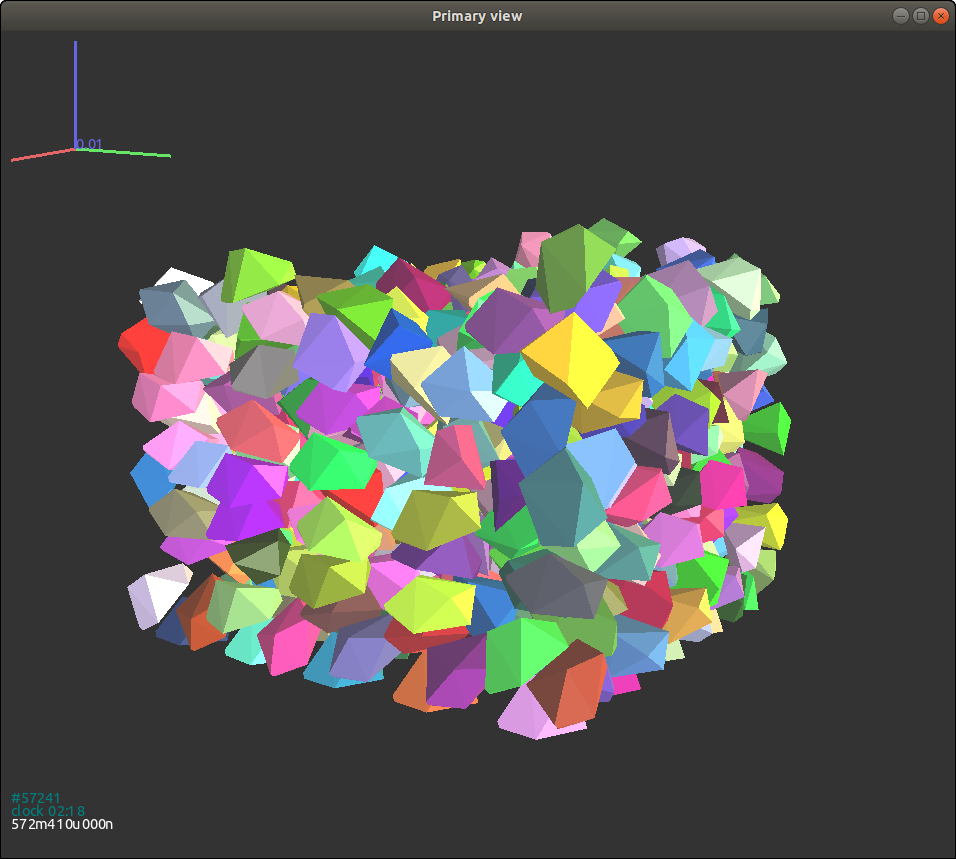Final packing of polyhedrons without random initial orientations (the box not shown). {#figgjkpolyhedron width=“8cm”}

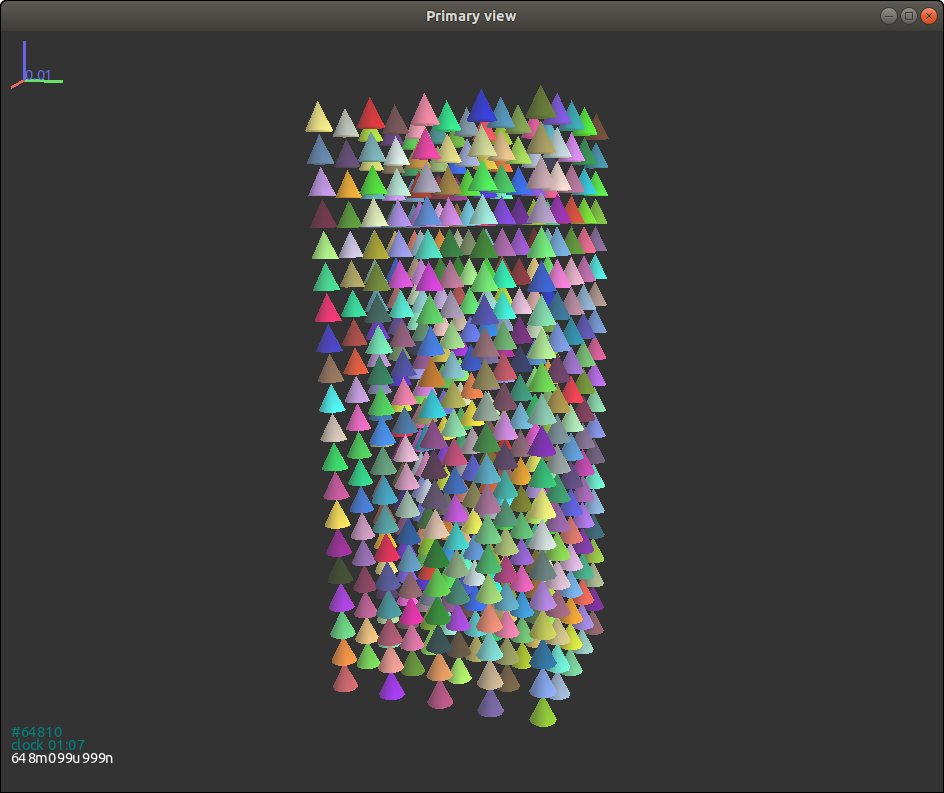Final packing of cones without random initial orientations (the box not shown). {#figgjkcone width=“8cm”}

对于圆锥体来说函数 GenSample 需做如下改动:

1
2
3
4
5
6
7

#生成试样
def GenSample(r,pos):
   for p in pos:
        body = GJKCone(0.005,0.01,0.05*1e-2,p_mat, False)
        body.state.pos=p
        O.bodies.append(body)   
        O.bodies[-1].shape.color=(rand.random(), rand.random(), rand.random())

Fig. 3.12{reference-type=“ref” reference=“figgjkcone”} 给出了固定初始朝向的圆锥体试样 (通过将变量 rotate 设置为 False 来取消随机的初始朝向生成)。 可以看到所有颗粒的初始状态都是完全相同的。

用户可以尝试将变量 rotate 设置为 True 来测试下随机初始朝向的颗粒试样:

1

body = GJKCone(0.005,0.01,0.05*1e-2,p_mat,True)

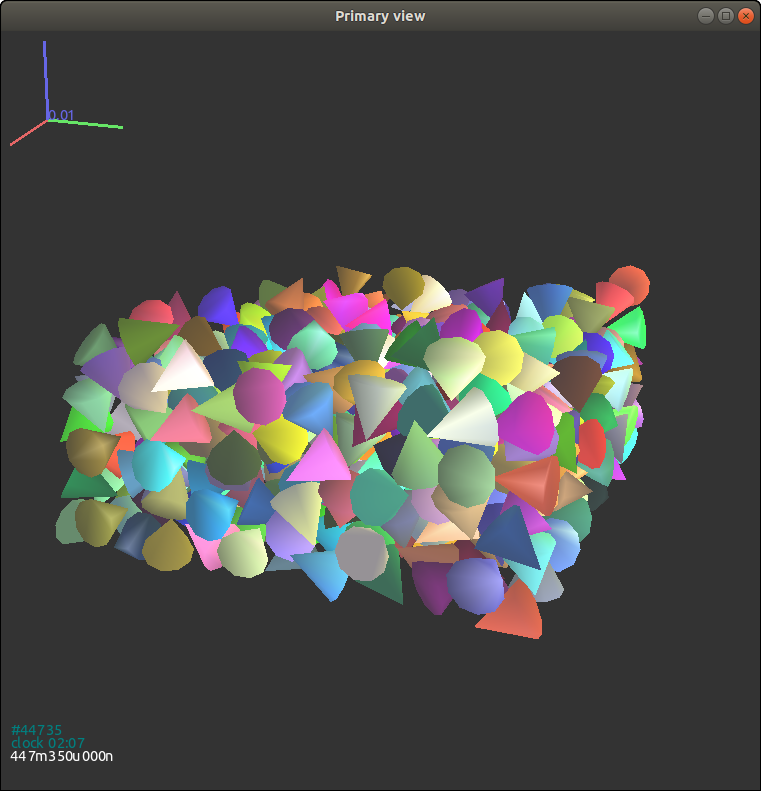Final packing of cones with random initial orientations (the box not shown). {#figgjkcone2 width=“8cm”}

如图所示，自由落体过程破坏了颗粒非常一致的初始朝向分布： 3.13{reference-type=“ref” reference=“figgjkcone2”}

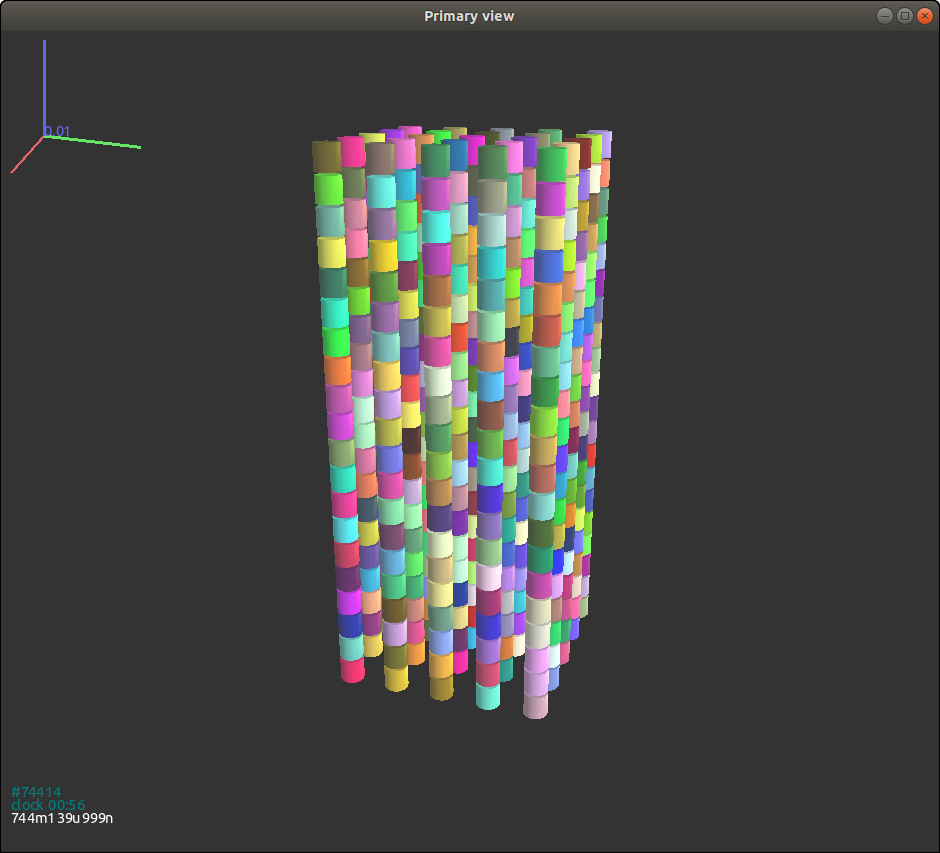Final packing of cylinders without random initial orientations (the box not shown). {#figgjkcylinder width=“8cm”}

圆柱的生成函数 GenSample 改动如下:

1
2
3
4
5
6

def GenSample(r,pos):
   for p in pos:
        body = GJKCylinder(0.005,0.01,0.05*1e-2,p_mat,False)
        body.state.pos=p
        O.bodies.append(body)   
        O.bodies[-1].shape.color=(rand.random(), rand.random(), rand.random())

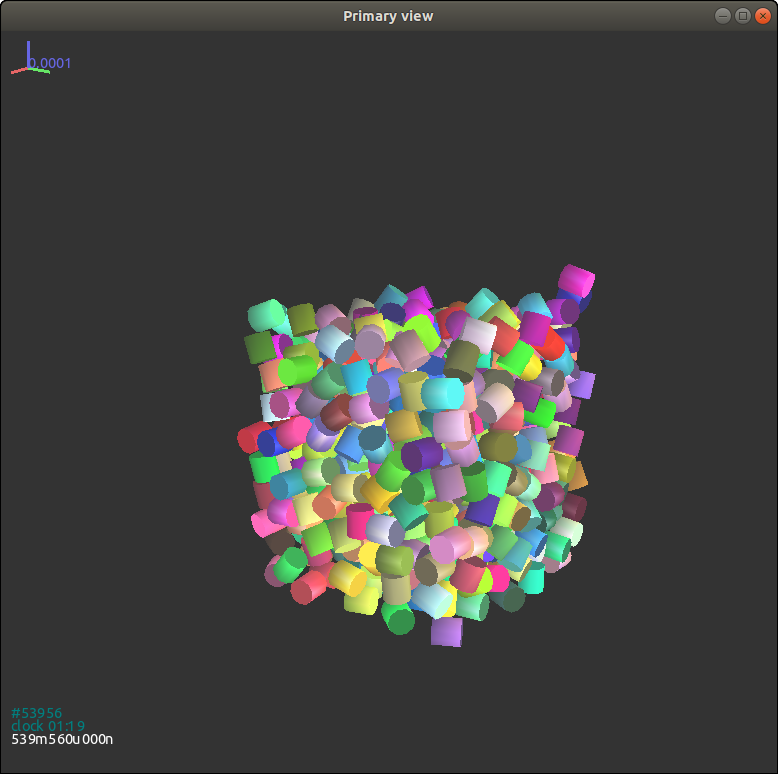Final packing of cylinders with random initial orientations (the box not shown). {#figgjkcylinder2 width=“8cm”}

不出意料，对于初始朝向一致的圆柱颗粒，即使是在自由落体后，它们的朝向仍然不变 Fig. 3.14{reference-type=“ref” reference=“figgjkcylinder”}。但是当初始朝向是随机生成时，自由落体结束后的圆柱体朝向变得不规律起来 3.15{reference-type=“ref” reference=“figgjkcylinder2”}。

1

body = GJKCylinder(0.005,0.01,0.05*1e-2,p_mat,True)

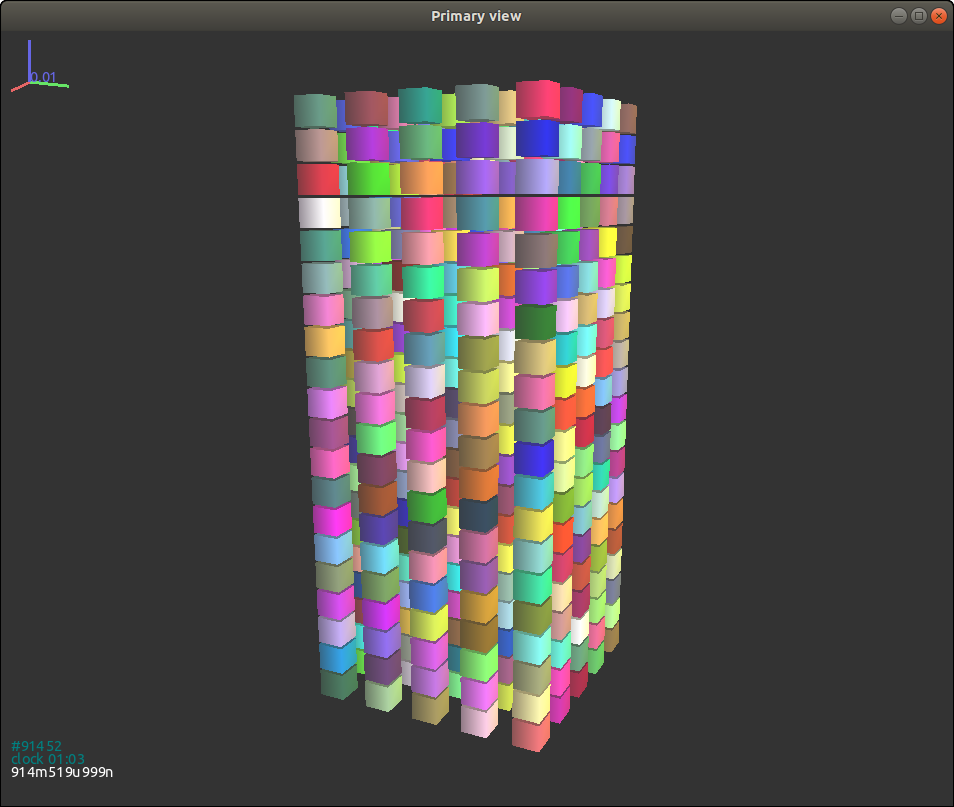Final packing of cuboids without random initial orientations (the box not shown). {#figgjkcuboid width=“8cm”}

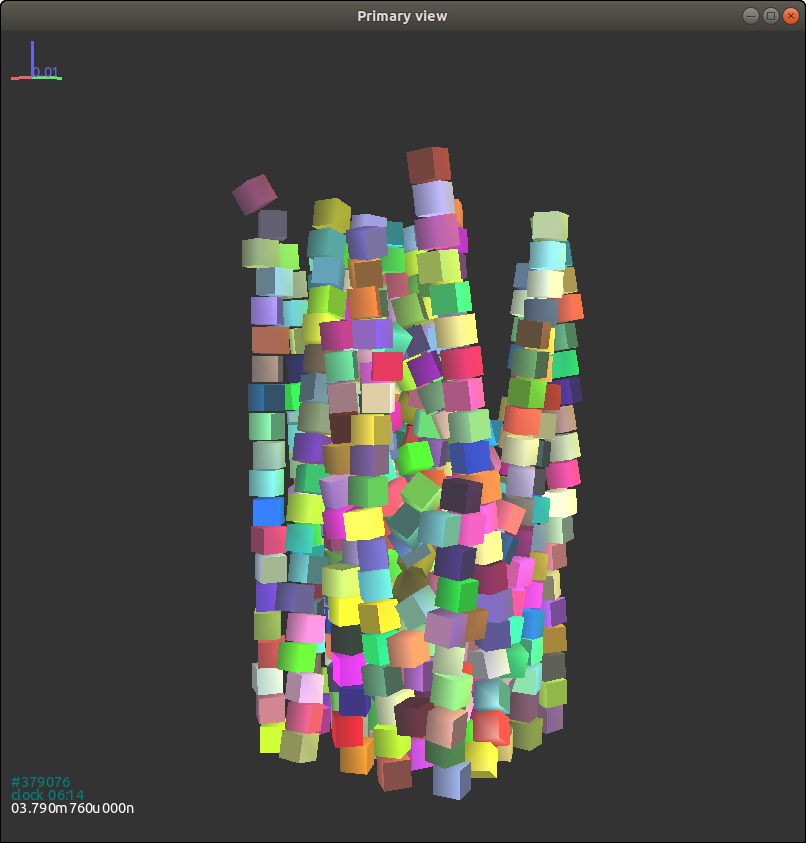Final packing of cuboids with random initial orientations (the box not shown). {#figgjkcuboid2 width=“8cm”}

立方体的函数如下:

1
2
3
4
5
6
7

#生成试样
def GenSample(r,pos):
   for p in pos:
        body = GJKCuboid([0.005,0.005,0.005],0.05*1e-2,p_mat,False)
        body.state.pos=p
        O.bodies.append(body)   
        O.bodies[-1].shape.color=(rand.random(), rand.random(), rand.random())

立方体的初始一致或随机生成朝向的自由落体过程与圆柱体非常相似。在初始朝向一致时，如图所示Fig. 3.16{reference-type=“ref” reference=“figgjkcuboid”} 自由落体结束后朝向并未发生显著变化。 但是随机初始朝向的试样，在自由落体过程前后的朝向分布有巨大的差异。 True as follows:

1

body = GJKCuboid([0.005,0.005,0.005],0.05*1e-2,p_mat,True)

另外，考虑到立方体颗粒间的间隙较小，所以它们的随机朝向在自由落体前后的分布差异较圆柱体不明显。

5 - 示例 4: 组合超级椭球的堆积模拟

该示例用于组合超级椭球的堆积模拟

组合超级椭球有形如真实颗粒(砂土)的如下显著的特性 (例如， 平直度，非对称性以及棱角度)。 组合超级椭球的形状函数可以通过组装八个超级椭球的形状参数得到: $$\Big(\big|\frac{x}{r_{x}}\big|^{\frac{2}{\epsilon_{1}}} + \big|\frac{y}{r_{y}}\big|^{\frac{2}{\epsilon_{1}}}\Big)^{\frac{\epsilon_{1}}{\epsilon_{2}}} +\big |\frac{z}{r_{z}}\big|^{\frac{2}{\epsilon_{2}}} = 1$$

::: {.subequations} $$\begin{aligned} r_{x} = r_x^+ \quad{}\text{if}\quad{} x\geq 0 \quad{}\text{else}\quad{} r_x^- \label{appa} \ r_{y} = r_y^+ \quad{}\text{if}\quad{} y\geq 0 \quad{}\text{else}\quad{} r_y^- \label{appb} \ r_{z} = r_z^+ \quad{}\text{if}\quad{} z\geq 0 \quad{}\text{else}\quad{} r_z^- \label{appc}\end{aligned}$$ :::

其中 $r_x^+,r_y^+,r_z^+$ 和 $r_x^-,r_y^-,r_z^-$ 分别表示颗粒在正负主轴 x, y, z 的长度; $\epsilon_1, \epsilon_2$ 控制颗粒表面的棱角度, 对于凸颗粒来说，它们取值范围在 $(0,2)$。 图 Fig. 3.18{reference-type=“ref” reference=“figmultipolysuper”} 形象的描述了 $\epsilon_1$ 和 $\epsilon_2$ 是如何影响颗粒形状的。 Python包 _superquadrics_utils 提供了两个用来生成组合超级椭球的函数 (参见 Sec. 5.1.2{reference-type=“ref” reference=“modsuperquadrics”}):

  • NewPolySuperellipsoid(eps, rxyz, mat, rotate, isSphere, inertiaScale = 1.0)

  • NewPolySuperellipsoid_rot(eps, rxyz, mat, $q_w$, $q_x$, $q_y$, $q_z$, isSphere, inertiaScale = 1.0)

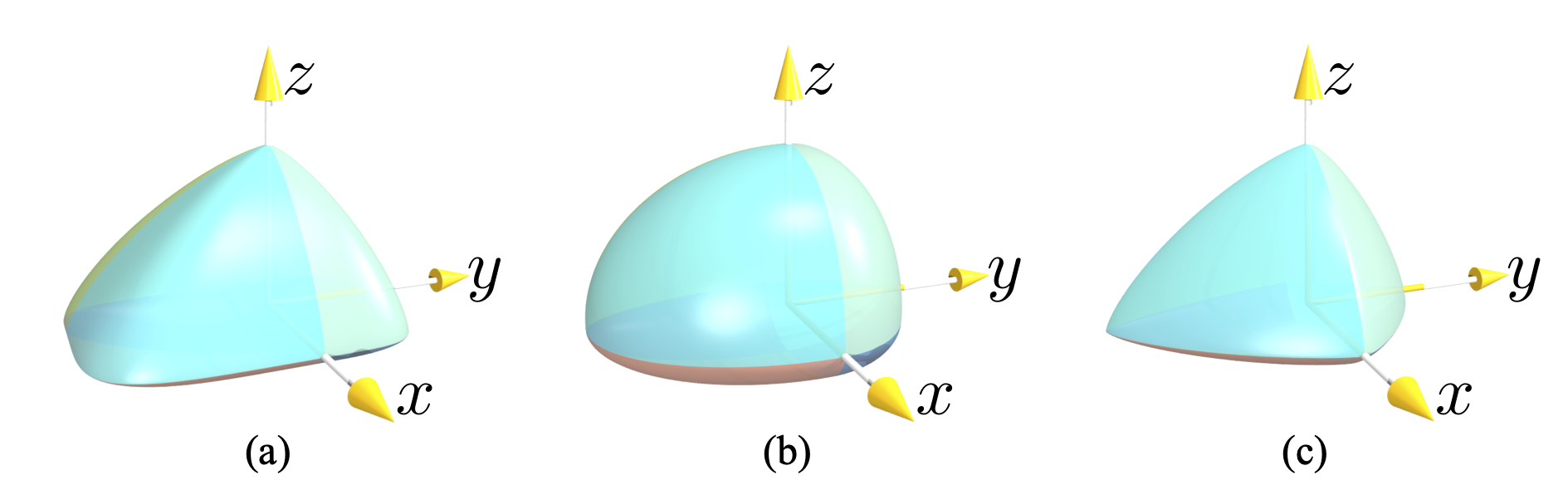组合超级椭球及其形状参数 $r_x^+=1.0, r_x^-=0.5, r_y^+=0.8, r_y^- = 0.9, r_z^+ = 0.4, r_z^- = 0.6$ (a) $\epsilon_1=0.4, \epsilon_2=1.5$, (b) $\epsilon_1=\epsilon_2=1.0$, (c) $\epsilon_1=\epsilon_2=1.5$.

这里我们给出了组合超级椭球堆积模拟的示例脚本:

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118

#
from sudodem._superquadrics_utils import *
import math
import random
import numpy as np

a=1.1734e-2
isSphere=False 
ap=0.4
eps=0.5
num_s=200
num_t=8000
trials=0


wallboxsize=[10e-1,0,0] #颗粒生成的盒子大小
boxsize=np.array([7e-1,7e-1,20e-1])

def down():
    for b in O.bodies:
        if(isinstance(b.shape,PolySuperellipsoid)):
            if(len(b.intrs())==0):
                b.state.vel=[0,0,-2]
                b.state.angVel=[0,0,0]
    
def gettop():
    zmax=0
    for b in O.bodies:
        if(isinstance(b.shape,PolySuperellipsoid)):
            if(b.state.pos[2]>=zmax):
                zmax=b.state.pos[2]
    return zmax


def Genparticles(a,eps,ap,mat,boxsize,num_s,num_t,bottom):
    global trials
    gap=max(a,a*ap)
    #print(gap)
    num=0
    coor=[]
    width=(boxsize[0]-2.*gap)/2.
    length=(boxsize[1]-2.*gap)/2.
    height=(boxsize[2]-2.*gap)
    #iteration=0
    
    while num<num_s and trials<num_t:
        isOK=True
        pos=[0]*3
        pos[0]=random.uniform(-width,width)
        pos[1]=random.uniform(gap-length,length-gap)
        pos[2]=random.uniform(bottom+gap,bottom+gap+height) 
          
        for i in range(0,len(coor)):
            distance=sum([((coor[i][j]-pos[j])**2.) for j in range(0,3)])
            if(distance<(4.*gap*gap)):
                
                isOK=False
                break
        
        if(isOK==True):        
            coor.append(pos)
            num+=1
            trials+=1
            #print(num)
    return coor 
               
    
def Addlayer(a,eps,ap,mat,boxsize,num_s,num_t):
   bottom=gettop()   
   coor=Genparticles(a,eps,ap,mat,boxsize,num_s,num_t,bottom)
   for b in coor:
      #xyz = np.array([1.0,0.5,0.8,1.5,1.2,0.4])*0.1
      xyz = np.array([1.0,0.5,0.8,1.5,0.2,0.4])*0.1
      bb=NewPolySuperellipsoid([1.0,1.0],xyz,mat,True,isSphere)#
      bb.state.pos=[b[0],b[1],b[2]]
      bb.state.vel=[0,0,-1]
      O.bodies.append(bb)   
   down()



p_mat = PolySuperellipsoidMat(label="mat1",Kn=1e5,Ks=7e4,frictionAngle=math.atan(0.3),density=2650,betan=0,betas=0) #define Material with default values
wall_mat = PolySuperellipsoidMat(label="wallmat",Kn=1e6,Ks=7e5,frictionAngle=0.0,betan=0,betas=0) #define Material with default values
wallmat_b = PolySuperellipsoidMat(label="wallmat",Kn=1e6,Ks=7e5,frictionAngle=math.atan(1),betan=0,betas=0) #define Material with default values

O.materials.append(p_mat)
O.materials.append(wall_mat)
O.materials.append(wallmat_b)


O.bodies.append(utils.wall(-0.5*wallboxsize[0],axis=0,sense=1, material = wall_mat))#left x
O.bodies.append(utils.wall(0.5*wallboxsize[0],axis=0,sense=-1, material = wall_mat))#right x
O.bodies.append(utils.wall(-0.5*boxsize[1],axis=1,sense=1, material = wall_mat))#front y
O.bodies.append(utils.wall(0.5*boxsize[1],axis=1,sense=-1, material = wall_mat))#back y
	
O.bodies.append(utils.wall(0,axis=2,sense=1, material =wallmat_b))#bottom z
#O.bodies.append(utils.wall(boxsize[0],axis=2,sense=-1, material = wallmat_b))#top z

newton=NewtonIntegrator(damping = 0.3,gravity=(0.,0.,-9.8),label="newton",isSuperquadrics=2)#isSuperquadrics=2 for Poly-superellipsoids

O.engines=[
   ForceResetter(),
   InsertionSortCollider([Bo1_PolySuperellipsoid_Aabb(),Bo1_Wall_Aabb()],verletDist=0.2*0.1),
   InteractionLoop(
      [Ig2_Wall_PolySuperellipsoid_PolySuperellipsoidGeom(), Ig2_PolySuperellipsoid_PolySuperellipsoid_PolySuperellipsoidGeom()], 
      [Ip2_PolySuperellipsoidMat_PolySuperellipsoidMat_PolySuperellipsoidPhys()], # collision "physics"
      [PolySuperellipsoidLaw()]   # 接触力本构模型
   ),
   newton
]
O.dt=5e-5
#生成颗粒
Addlayer(a,eps,ap,p_mat,boxsize,num_s,num_t)#Note: these particles may intersect with each other when we generate them.

#显示设置。用户可以通过界面窗口来直接更改对应设置。
sudodem.qt.Gl1_PolySuperellipsoid.wire=False
sudodem.qt.Gl1_PolySuperellipsoid.slices=10
sudodem.qt.Gl1_Wall.div=0 #hide the walls

图 3.19{reference-type=“ref” reference=“figpolysuperpacking”} 给出了组合超级椭球堆积模拟的结果示意图。

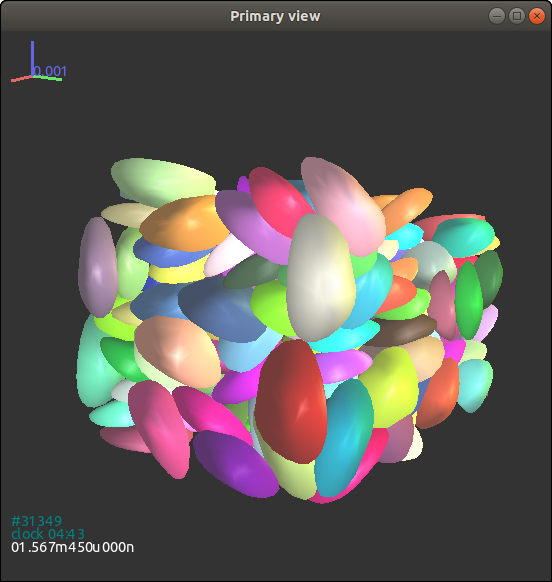Packing of poly-superellipsoids. {#figpolysuperpacking width=“10cm”}

6 - 示例 5: 超椭圆堆积模拟

该示例给出了超椭圆的堆积模拟 (超级椭球的二维形状)

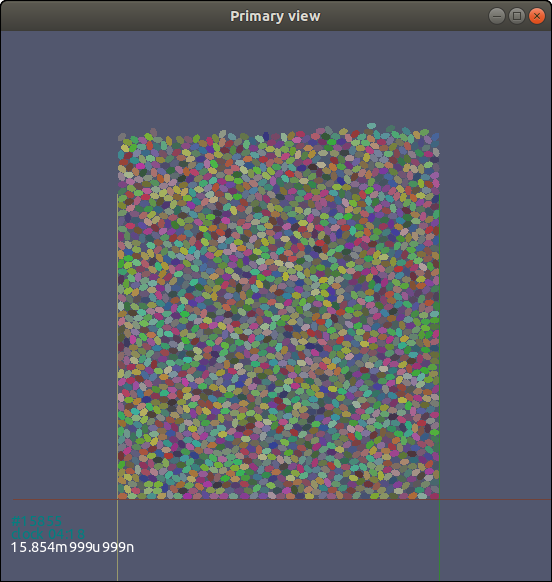
超椭圆局部坐标系下的形状函数如下式： $$\big|\frac{x}{r_x}\big|^{\frac{2}{\epsilon}} + \big|\frac{y}{r_y}\big|^{\frac{2}{\epsilon}} = 1$$ 其中 $r_x$ 和 $r_y$ 分别表示x和y轴的半长轴长度; $\epsilon \in (0, 2)$ 控制了颗粒表面的棱角度。 我们这里给出了超椭圆在重力作用下自由落体堆积的模拟脚本:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94

##################################################
from sudodem import utils
from sudodem._superellipse_utils import *
import numpy as np
import math
import random 
random.seed(11245642)
####################################################
#########设置
####################################################
isSphere = False

r = 0.5 #颗粒大小
num_s=100
num_t=8000
trials=0
boxsize=[50.0,10.0]

#############################
mat =SuperellipseMat(label="mat1",Kn=1e8,Ks=7e7,frictionAngle=math.atan(0.225),density=2650)
O.materials.append(mat)

O.bodies.append(utils.wall(-0.5*boxsize[1],axis=1,sense=1, material = 'mat1'))#ground 
O.bodies.append(utils.wall(-0.5*boxsize[0],axis=0,sense=1, material = 'mat1'))#left
O.bodies.append(utils.wall(0.5*boxsize[0],axis=0,sense=-1, material = 'mat1'))#right

###
def gettop():
    ymax=0
    for b in O.bodies:
        if(isinstance(b.shape,Superellipse)):
            if(b.state.pos[1]>=ymax):
                ymax=b.state.pos[1]
    return ymax


def Genparticles(r,mat,boxsize,num_s,num_t,bottom):
    global trials
    gap=r
    #print(gap)
    num=0
    coor=[]
    width=(boxsize[0]-2.*gap)/2.
    height=(boxsize[1]-2.*gap)
    #iteration=0
    
    while num<num_s and trials<num_t:
        isOK=True
        pos=[0]*2
        pos[0]=random.uniform(-width,width)
        pos[1]=random.uniform(bottom+gap,bottom+gap+height) 
          
        for i in range(0,len(coor)):
            distance=sum([((coor[i][j]-pos[j])**2.) for j in range(0,2)])
            if(distance<(4.*gap*gap)):
                
                isOK=False
                break
        
        if(isOK==True):        
            coor.append(pos)
            num+=1
            trials+=1
            #print(num)
    return coor 
                 

def Addlayer(r,mat,boxsize,num_s,num_t):
    bottom=gettop()   
    coor=Genparticles(r,mat,boxsize,num_s,num_t,bottom)
    for b in coor:
        rr = r*random.uniform(0.5,1.0)
        bb = NewSuperellipse(1.5*r,r,1.0,mat,True,isSphere)
        bb.state.pos=b
        bb.state.vel=[0,-1]
        O.bodies.append(bb)  
	if len(O.bodies) - 3 > 2000:
		O.engines[-1].dead=True 

O.dt = 1e-3

newton=NewtonIntegrator(damping = 0.1,gravity=(0.,-10.0),label="newton",isSuperellipse=True)

O.engines=[
   ForceResetter(),
   InsertionSortCollider([Bo1_Superellipse_Aabb(),Bo1_Wall_Aabb()],verletDist=0.1),
   InteractionLoop(
      [Ig2_Wall_Superellipse_SuperellipseGeom(), Ig2_Superellipse_Superellipse_SuperellipseGeom()], 
      [Ip2_SuperellipseMat_SuperellipseMat_SuperellipsePhys()], # 接触检测引擎
      [SuperellipseLaw()]   # 接触力本构模型
   ),
   newton,
   PyRunner(command='Addlayer(r,mat,boxsize,num_s,num_t)',virtPeriod=0.1,label='check',dead = False)
]

如上脚本需使用 sudodem2d 运行，模拟结果如图所示 Fig. 3.20{reference-type=“ref” reference=“figpackingellipse”}。

Packing of superellipses under gravity. {#figpackingellipse width=“10cm”}