3.2. 球簇离散元模型¶
3.2.1. 球簇颗粒¶
球簇颗粒是由一系列球(以下简称组成球)捆绑构建出的非球颗粒,主要分两种类型(见 图 3.1 ):一种是组成球间可以有重叠,也被称为clump模型;另一种是组成球之间无重叠,也被称为cluster模型。注,此处的重叠表示远大于DEM中颗粒正常接触的重叠。以上两种球簇模型的分类主要基于下述实践目的:clump模型可单纯用于表示非球颗粒,不涉及内部组成球间的接触力计算;cluster模型则涉及组成球间的接触力计算,即颗粒内部力可求解,该模型往往被用于考虑颗粒破碎的模拟。
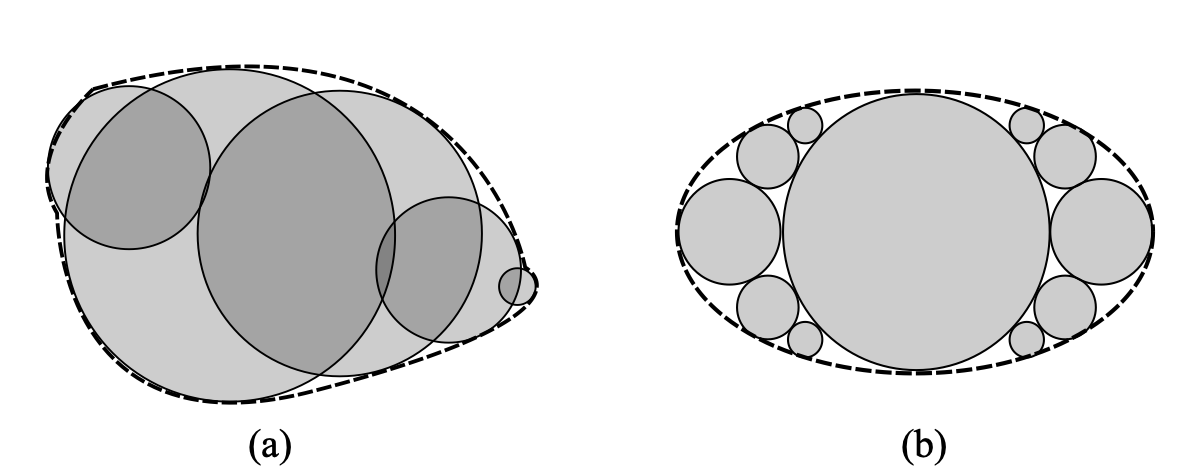
图 3.1 两类球簇模型的二维示意图:(a) clump模型;(b) cluster模型¶
由球簇颗粒的定义可知,目标非球颗粒形状的逼近程度直接与组成球的个数相关。一般地,组成球的个数越多,球簇颗粒越能够逼近目标颗粒。此外,球簇颗粒中组成球的排布可以是任意的,因此,球簇模型具有很大的灵活性。理论上,球簇颗粒模型可以用于构建任意复杂形状的颗粒。但是,在实践过程中,组成球数量较大会显著地增加模拟计算耗时。鉴于此,有学者 [1] 对非球颗粒球簇模型的构建进行了相关研究,尝试尽可能使用较少的组成球来构建颗粒。
3.2.2. 接触计算¶
球簇颗粒的接触检测是基于组成球的接触检测,即通过检测两颗粒的组成球的接触来实现颗粒接触检测,从而大大降低了非球颗粒间的接触检测的复杂度。组成球间的颗粒接触检测(如 图 3.2 (b))与球形离散单元模型中的接触检测(如 图 3.2 (a))完全相同。但需要指出的是,为了加速接触检测,属于同一颗粒的组成球间可以不用进行接触检测(只针对clump模型)。球形颗粒间的距离当且仅当满足以下条件时两颗粒间存在接触:
式中,\(d_{ij}\) 为两球形颗粒质心间的距离;\(R_i\) 和 \(R_j\) 分别为两颗粒的半径。对于相互接触的两球形颗粒,颗粒间的接触重叠量(一般为接触嵌入深度):math:delta 则为:
其他接触几何量亦可容易地获取,如接触法向定义为两颗粒质心连线所在方向,此处从略。值得强调的是,此处以及本文后续章节均只涉及非粘性颗粒间的接触;对于粘性颗粒间的接触,式( (3.12) )则需要考虑颗粒间可能存在一定的间隙,从而式( (3.13) )中的 \(\delta\) 可以取负值,即模拟颗粒分离后的粘性力。
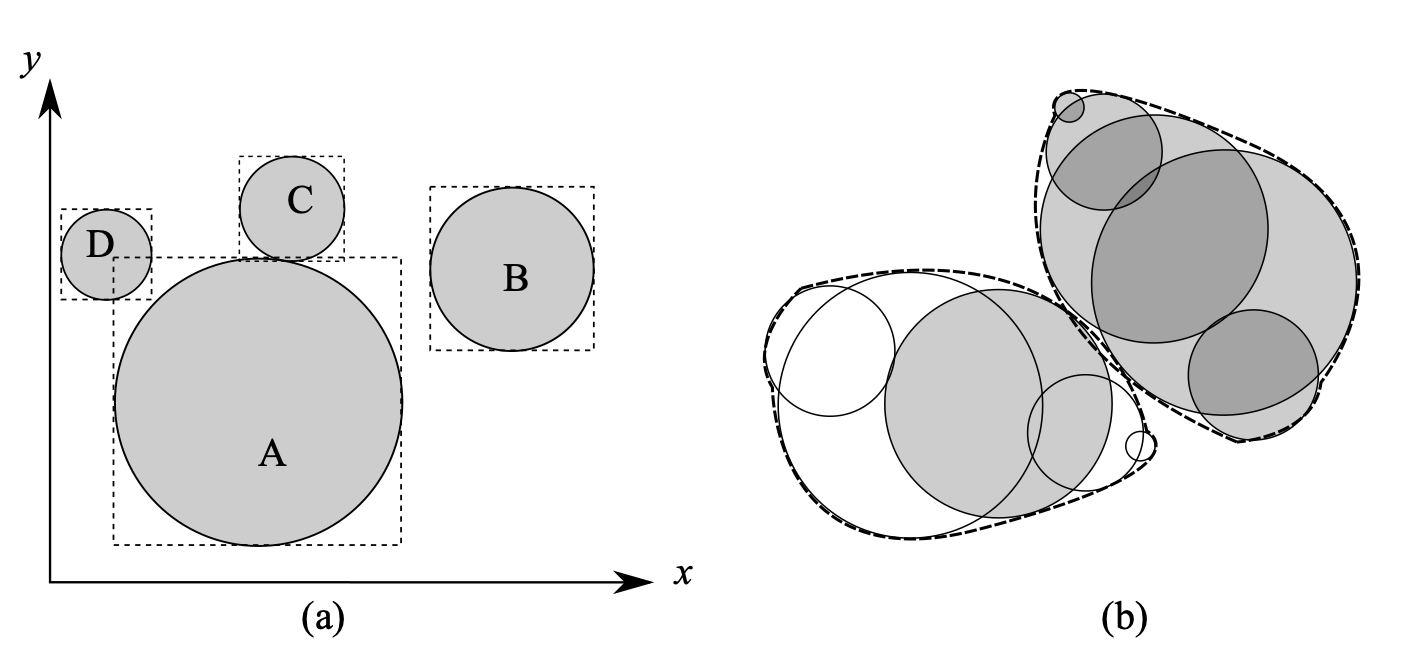
图 3.2 球形颗粒(a) 、球簇颗粒(b)的接触检测二维示意图¶
需要指出的是,在每一DEM计算循环中需要进行大量颗粒间的接触检测,而每一颗粒只与其周围的少数(相对于系统中的大量颗粒)颗粒存在接触,亦即某一给定颗粒与绝大多数颗粒是无接触的。因此,为了避免对这些大量的非接触的颗粒对使用式( (3.12) )进行精确的接触检测判断,通常需要先利用筛除算法(sweep and prune) [2] 排除这些大量的非接触颗粒对。包围盒算法是一类有效的筛除方法,广泛使用的包围盒有球包围盒、轴对齐包围盒以及有向包围盒等。其中,轴对齐包围盒(axis-aligned bounding box,AABB) [2] 算法在DEM颗粒接触检测中最为流行。顾名思义,AABB是包围在物体外的一个六面与全局坐标轴对齐的立方体盒子,且在大多数情况下,AABB可以比较紧凑地包围颗粒。如 图 3.2 (a)所示,其中的矩形框即为轴对齐包围盒。通过比较每个轴上的投影的长度,便可检测两个AABB之间的重叠情况。如果存在使AABB的投影不重叠的轴(如 图 3.2 (a)中颗粒A和颗粒B的包围盒在x轴上的投影不重叠),则两个AABB之间不存在重叠,这也意味着两个颗粒之间不重叠。如果两个AABB之间存在重叠(如 图 3.2 (a)中颗粒A和颗粒C、颗粒D间存在AABB的重叠),则两个颗粒之间可能存在重叠(如 图 3.2 (a)中颗粒A与颗粒C接触而颗粒A与颗粒D不接触)。轴对齐包围盒算法能够排除所有类似颗粒A、B这样的颗粒对。
3.2.3. 接触模型¶
如前所述,球簇颗粒间的接触本质上是来自不同颗粒的组成球之间的接触。因此,传统球形离散单元的接触模型均可直接用于球簇离散单元模型。以接触刚度模型为例,我们可以灵活地选择线刚度模型、体积刚度模型以及其他非线性刚度模型(如简化的Hertz-Mindlin模型)。线刚度模型和体积刚度模型分别在本章后续小节中具体介绍,此处从略。
3.2.4. 参考文献¶
Alaa K Ashmawy, V Vinh Hoang, Beena Sukumaran, and others. Evaluating the influence of particle shape on liquefaction behavior using discrete element modeling. In The 13th International Offshore and Polar Engineering Conference, volume 2, 542–549. Honolulu, 2003. International Society of Offshore and Polar Engineers.
David Baraff. Dynamic simulation of non-penetrating rigid bodies. PhD thesis, Cornell University, Ithaca, NY, USA, 1992.
Gino van den Bergen. Efficient collision detection of complex deformable models using aabb trees. Journal of Graphics Tools, 2(4):1–13, 1997.