3.5. 扩展超椭球离散元模型

3.5.1. 扩展超椭球

扩展超椭球（Poly-Superellipsoid） [8] 可以表征丰富的形状特征，包括伸长率、平整度、棱角度和非对称性等。如 图 3.9 所示，一个扩展超椭球由八个八分之一超椭球组合而成，其表面方程定义如下：

\[\Big(\big|\frac{x}{r_{xi}}\big|^{\frac{2}{\epsilon_{1i}}} + \big|\frac{y}{r_{yi}}\big|^{\frac{2}{\epsilon_{1i}}}\Big)^{\frac{\epsilon_{1i}}{\epsilon_{2i}}} +\big |\frac{z}{r_{zi}}\big|^{\frac{2}{\epsilon_{2i}}} = 1\]

其中， \(r_{xi}, r_{yi}, r_{zi}, \epsilon_{1i}, \epsilon_{2i} (i=1,\dots,8)\) 是第 \(i\) 个超椭球的形状参数，总共合计40个形状参数。为减少参数，根据连续和光滑条件，引入如下约束：

\[\epsilon_{1i} = \epsilon_1,\quad{}\epsilon_{2i}=\epsilon_2\]

和

\[\begin{split}r_{x1} =& r_{x4} = r_{x5} = r_{x8} = r_x^+, (x\geq 0)\\ r_{x2} =& r_{x3} = r_{x6} = r_{x7} = r_x^-, (x< 0)\\ r_{y1} =& r_{y2} = r_{y5} = r_{y6} = r_y^+, (y\geq 0)\\ r_{y3} =& r_{y4} = r_{y7} = r_{y8} = r_y^-, (y< 0)\\ r_{z1} =& r_{z2} = r_{z3} = r_{z4} = r_z^+, (z\geq 0)\\ r_{z5} =& r_{z6} = r_{z7} = r_{z8} = r_z^-, (z< 0)\end{split}\]

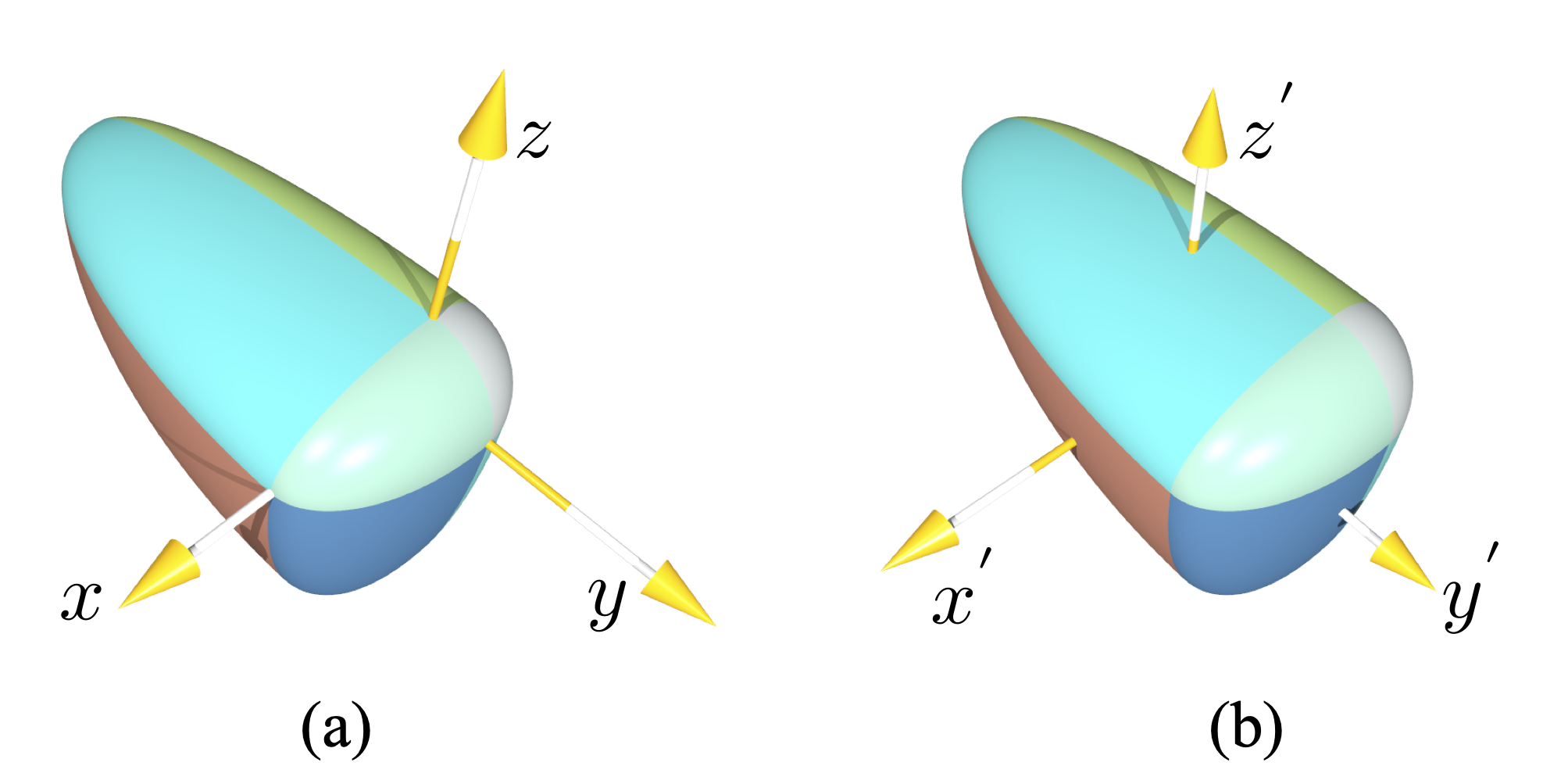
图 3.9 在局部坐标系中的扩展超椭球 (\(r_x^+=1.0, r_x^-=0.5, r_y^+=0.5, r_y^- = 2.5, r_z^+ = 0.5, r_z^- = 1.7\) 及 \(\epsilon_1=\epsilon_2=1.0\))： (a) 坐标原点在几何中心， (b) 坐标原点在质量中心。

因此，总共只需要八个参数来控制扩展超椭球的形状，其中 \(r_x^+,r_y^+,r_z^+\) 和 \(r_x^-,r_y^-,r_z^-\) 控制颗粒分别在正半轴和负半轴的伸长，以及 \(\epsilon_i (i=1,2)\) 控制曲面的方形度。 经过改变 \(\epsilon_i\)，我们得到形状各异的扩展超椭球，参见 图 3.10 。为了讨论方便，定义两局部笛卡尔坐标系：

• 一是原点在几何中心如 图 3.9(a)所示；

• 二是原点在质心如 图 3.9 (b)所示。

两个坐标之间的变换很容易给出，

\[x^{'} = x - x_c,\quad{} y^{'} = y - y_c,\quad{} z^{'} = z - z_c\]

其中 \(x_c, y_c, z_c\) 为在坐标系 \(XYZ\) 中的质心坐标，式 (3.32) 。下文局部坐标系默认采用原点在几何中心，除非另有说明。

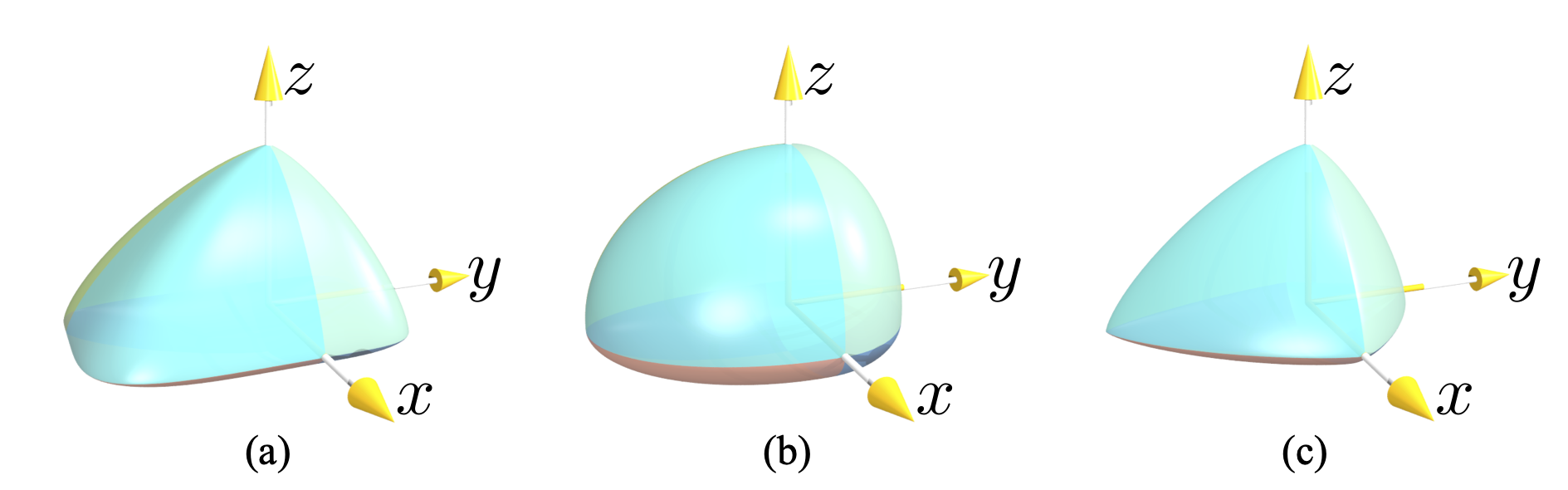
图 3.10 扩展超唾弃：\(r_x^+=1.0, r_x^-=0.5, r_y^+=0.8, r_y^- = 0.9, r_z^+ = 0.4, r_z^- = 0.6\) 及 (a) \(\epsilon_1=0.4, \epsilon_2=1.5\), (b) \(\epsilon_1=\epsilon_2=1.0\), (c) \(\epsilon_1=\epsilon_2=1.5\).

图 3.11 随机形状参数的扩展超椭球

图 3.12 扩展超椭球拟合真实形状颗粒举例: (a) \(\epsilon_1 = 0.85, \epsilon_2 = 1.0, r_x^+ = 3.26, r_x^- = 2.67, r_y^+ = 1.66, r_y^- = 1.59, r_z^+ = 1.81, r_z^- = 1.67\), (b) \(\epsilon_1 = 1.1, \epsilon_2 = 1.2, r_x^+ = 2.07, r_x^- = 1.02, r_y^+ = 1.26, r_y^- = 1.23, r_z^+ = 1.40, r_z^- = 0.35\).

图 3.11 显示了一些由扩展超椭球表示的颗粒形状示例。显然，基于扩展超椭球的方法可以提供对各种形状颗粒的灵活描述。实际上，它能够捕捉到真实颗粒的主要形状特征（非凸性可以通过聚集多个扩展超椭球来近似捕捉），包括扁平度、不对称性和角度。构建扩展超椭球的一种方法是直接拟合真实颗粒的点云来实现，这可以通过最小化以下给出的函数的误差来完成。

\[\min \sum_{k=0}^{N}\Bigg(\Big(\big|\frac{x_k}{r_{xi}}\big|^{\frac{2}{\epsilon_{1}}} + \big|\frac{y_k}{r_{yi}}\big|^{\frac{2}{\epsilon_{1}}}\Big)^{\frac{\epsilon_{1}}{\epsilon_{2}}} +\big |\frac{z_k}{r_{zi}}\big|^{\frac{2}{\epsilon_{2}}} - 1\Bigg)^2\]

其中 \(N\) 是点的数量；\(x_k, y_k, z_k\) 是以几何中心为原点的局部坐标系中第 \(k\) 个点的坐标。一般来说，总共有 14 个变量（八个用于颗粒形状的参数，三个用于颗粒中心，另外三个用于由三个欧拉角表示的颗粒方向），用于拟合任意点云数据。解决包含 14 个变量的如此大的非线性最小二乘问题可能看起来令人生畏，但实际上是可行的。可以首先进行一些预处理，以获得这些变量的更好初始值。例如，可以将点云与主轴对齐。此外，针对大型非线性最小二乘问题设计的开源求解器，例如 Ceres Solver 和 IPOPT，可以方便地用于解决这类优化问题。图 3.12 中展示了两个示例，其中点云已经与主轴对齐，以用作演示。

3.5.2. 支撑函数和支撑点

引入超椭球的参数方程：

(3.30)\[\begin{split}x &= \mathrm{Sign}(\cos\theta)r_x|\cos\theta|^{\epsilon_1}|\cos\phi|^{\epsilon_2} \\ y &= \mathrm{Sign}(\sin\theta)r_y|\sin\theta|^{\epsilon_1}|\cos\phi|^{\epsilon_2} \\ z &= \mathrm{Sign}(\sin\phi)r_z|\sin\phi|^{\epsilon_2}\end{split}\]

其中 \(\theta \in [0,2\pi),\phi \in [-\frac{\pi}{2},\frac{\pi}{2}]\) ， \(\mathrm{Sign}(x)\) 为符号函数。前述扩展超椭球方程可以更改成相应的参数方程。

由于扩展超椭球的凸性，我们可以构建一个从表面外法向量 \(\mathbf{n}(n_x, n_y, n_z)\) 到扩展超椭球表面点 \(\mathbf{p}(x, y, z)\) 的一对一映射函数 \(S(\mathbf{n})\)，其中 \(\mathbf{p}=S(\mathbf{n)}\)，根据方程 (3.30) 和 (3.25) (a,b)。这个函数给出了在 \(\mathbf{n}\) 方向上表面上最远的点，因此被称为支撑函数，它是一个凸函数。相应的最远点被称为支撑点，参见 图 3.13 。在数学上，\(S(\mathbf{n})=\sup\{\mathbf{n}\cdot \mathbf{p}|\mathbf{p}\in\Gamma\}\) ，其中 \(\Gamma\) 是颗粒表面。前面提到的方向向量 \(\mathbf{v}\)，即 图 3.13 中的 \(\mathbf{v}\)，位于颗粒的局部坐标系中，该坐标系随颗粒一起旋转。颗粒的方向由四元数 \(q(q_w,q_x,q_y,q_z)=\cos\frac{\hat\theta}{2}+(\hat{e}_x\mathbf{i}+\hat{e}_y\mathbf{j}+\hat{e}_z\mathbf{k})\sin\frac{\hat\theta}{2}\) 跟踪，其中 \(\hat\theta\) 是颗粒绕单位轴 \(\mathbf{\hat{e}}(\hat{e}_x,\hat{e}_y,\hat{e}_z)\) 旋转的角度。可以从 \(q\) 直接获得旋转矩阵 \(\mathbf{R}\)，因此对于给定的全局坐标系中的方向向量 \(\mathbf{\hat{v}}\)，局部支撑点为 \(S(\mathbf{R}^{-1}\mathbf{\hat{v}})\)，其中 \(\mathbf{R}^{-1}\) 是 \(\mathbf{R}\) 的逆矩阵。在基于常规法线方法的接触检测过程中，方程 (3.36) 中经常需要调用支撑函数 \(S(\mathbf{n})\)，这将在 接触及接触计算 中详细介绍。为了提高计算效率，不需要显式计算方程 (3.25) 中的 \(\theta\) 和 \(\phi\) ，因此支撑函数 \(S(\mathbf{n})\) 可以表示为

(3.31)\[\begin{split}x &= \frac{1}{2}\mathrm{Sign}(n_x) \big[(1+\mathrm{Sign}(n_x))r_x^++(1-\mathrm{Sign}(n_x))r_x^-\big] \alpha_1^{\epsilon_1/2}\alpha_2^{\epsilon_2/2}\\ y &= \frac{1}{2}\mathrm{Sign}(n_y) \big[(1+\mathrm{Sign}(n_y))r_y^++(1-\mathrm{Sign}(n_y))r_y^-\big] (1-\alpha_1)^{\epsilon_1/2}(1-\alpha_2)^{\epsilon_2/2}\\ z &= \frac{1}{2}\mathrm{Sign}(n_z) \big[(1+\mathrm{Sign}(n_z))r_z^++(1-\mathrm{Sign}(n_z))r_z^-\big] (1-\alpha_2)^{\epsilon_2/2}\end{split}\]

其中 \(\alpha_1\) 和 \(\alpha_2\) 分别等于 \(\cos^2(\theta)\) 和 \(\cos^2(\phi)\)，具体如下：

\[\begin{split}\alpha_1 = \begin{cases} \Big(1+\big|\frac{r_yn_y}{r_xn_x}\big|^{\frac{2}{2-\epsilon_1}}\Big)^{-1},& \text{if } n_x \neq 0, \\ 0,& \text{otherwise.} \end{cases}\end{split}\]

与

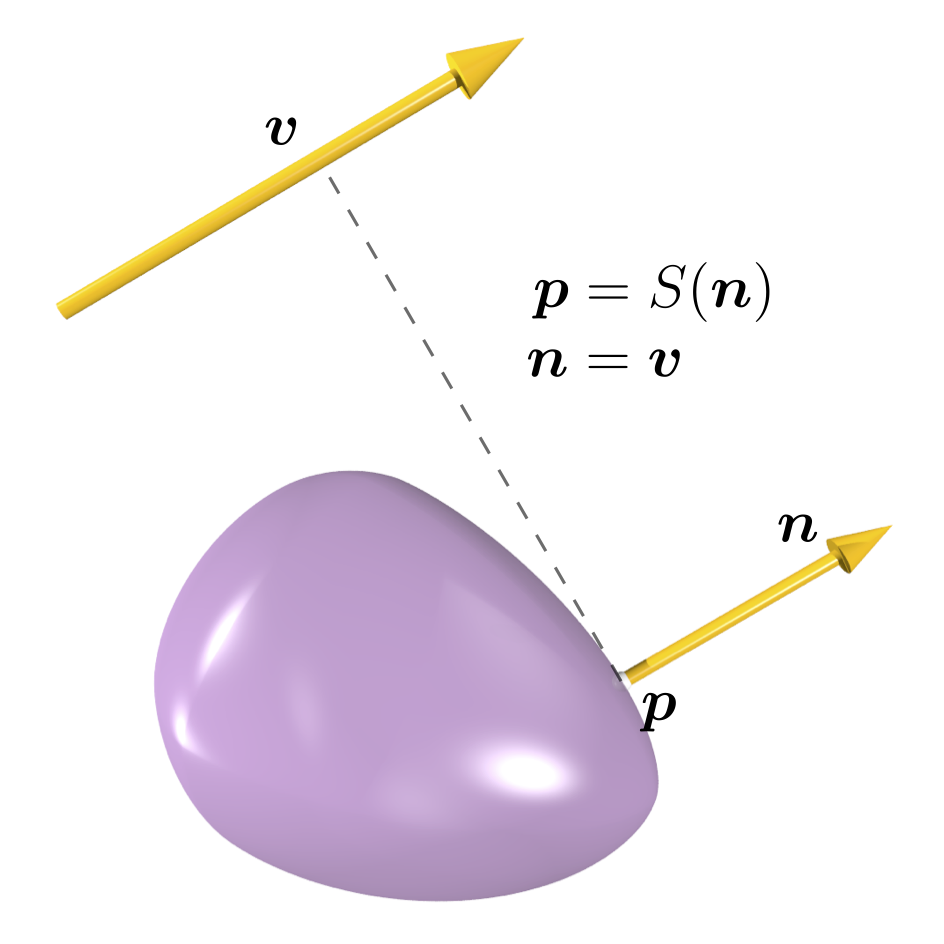
图 3.13 给定一个方向向量 \(\mathbf{v}\) 和一个支撑函数 \(S(\mathbf{n})\)，在颗粒表面上找到一个支撑点 \(\mathbf{p}\)。注意：\(\mathbf{n}\) 是支撑点 \(\mathbf{p}\) 处颗粒表面的外法线。

3.5.3. 颗粒参数

扩展超椭球的质心 \((x_c, y_c, z_c)\) 可以通过对所有八分体的质心进行加权求和来获得，具体表示为：

(3.32)\[\begin{split}\begin{aligned} x_c &= \frac{\sum_{i=1}^8x_{ci}m_i}{M}\\ y_c &= \frac{\sum_{i=1}^8y_{ci}m_i}{M}\\ z_c &= \frac{\sum_{i=1}^8z_{ci}m_i}{M}\end{aligned}\end{split}\]

与

(3.33)\[M = \sum_{i=1}^8 m_i\]

其中 \(M\) 是扩展超椭球颗粒的质量；\((x_{ci}, y_{ci}, z_{ci})\) 和 \(m_i\) 分别是第 \(i\) 个八分体的质心和质量，可以通过以下闭合形式获得：

及

\[\begin{split}\begin{array}{lll} S_{x1} & = S_{x4} = S_{x5} = S_{x8} = 1, \quad{} S_{x2} &= S_{x3} = S_{x6} = S_{x7} = -1\\ S_{y1} & = S_{y2} = S_{y5} = S_{y6} = 1, \quad{} S_{y3} &= S_{y4} = S_{y7} = S_{y8} = -1\\ S_{z1} & = S_{z2} = S_{z3} = S_{z4} = 1,\quad{} S_{z5} &= S_{z6} = S_{z7} = S_{z8} = -1 \end{array}\end{split}\]

与

\[m_i = \frac{1}{12}\rho r_{xi}r_{yi}r_{zi}\epsilon_1\epsilon_2B(\frac{1}{2}\epsilon_1, \frac{1}{2}\epsilon_1)B(\frac{1}{2}\epsilon_2, \epsilon_2)\]

其中 \(\rho\) 是材料的质量密度；项 \(B(x, y)\) 是一个被定义为以下形式的 beta 函数：

\[B(x, y) = 2\int_0^{\pi/2}\mathrm{sin}^{2x-1}\phi \mathrm{cos}^{2y-1}\phi d\phi\]

一个八分体超椭球的主惯性矩由以下方式确定：

其中 \(\beta_1\) 和 \(\beta_2\) 由下式给出：

\[\begin{split}\left\{ \begin{array}{l@{}l} \beta_1 = B(\frac{3}{2}\epsilon_1, \frac{1}{2}\epsilon_1)B(\frac{1}{2}\epsilon_2, 2\epsilon_2 + 1)\\ \beta_2 = B(\frac{1}{2}\epsilon_1, \frac{1}{2}\epsilon_1 + 1)B(\frac{3}{2}\epsilon_2,\epsilon_2+1) \end{array} \right.\end{split}\]

因此，扩展超椭球颗粒的主惯性矩可以表示为：

\[\begin{split}\begin{array}{l@{}l} I_{xx}^c = \sum_{i=1}^8 I_{xx}^{(i)}\\ I_{yy}^c = \sum_{i=1}^8 I_{yy}^{(i)}\\ I_{zz}^c = \sum_{i=1}^8 I_{zz}^{(i)} \end{array}\end{split}\]

根据平行轴定理，扩展超椭球的主惯性矩在以质心为原点的局部坐标系中表示为：

(3.34)\[\begin{split}\begin{array}{l@{}l} I_{xx} = I_{xx}^c -(y_c^2+z_c^2)M\\ I_{yy} = I_{yy}^c -(x_c^2+z_c^2)M\\ I_{zz} = I_{zz}^c -(x_c^2+y_c^2)M \end{array}\end{split}\]

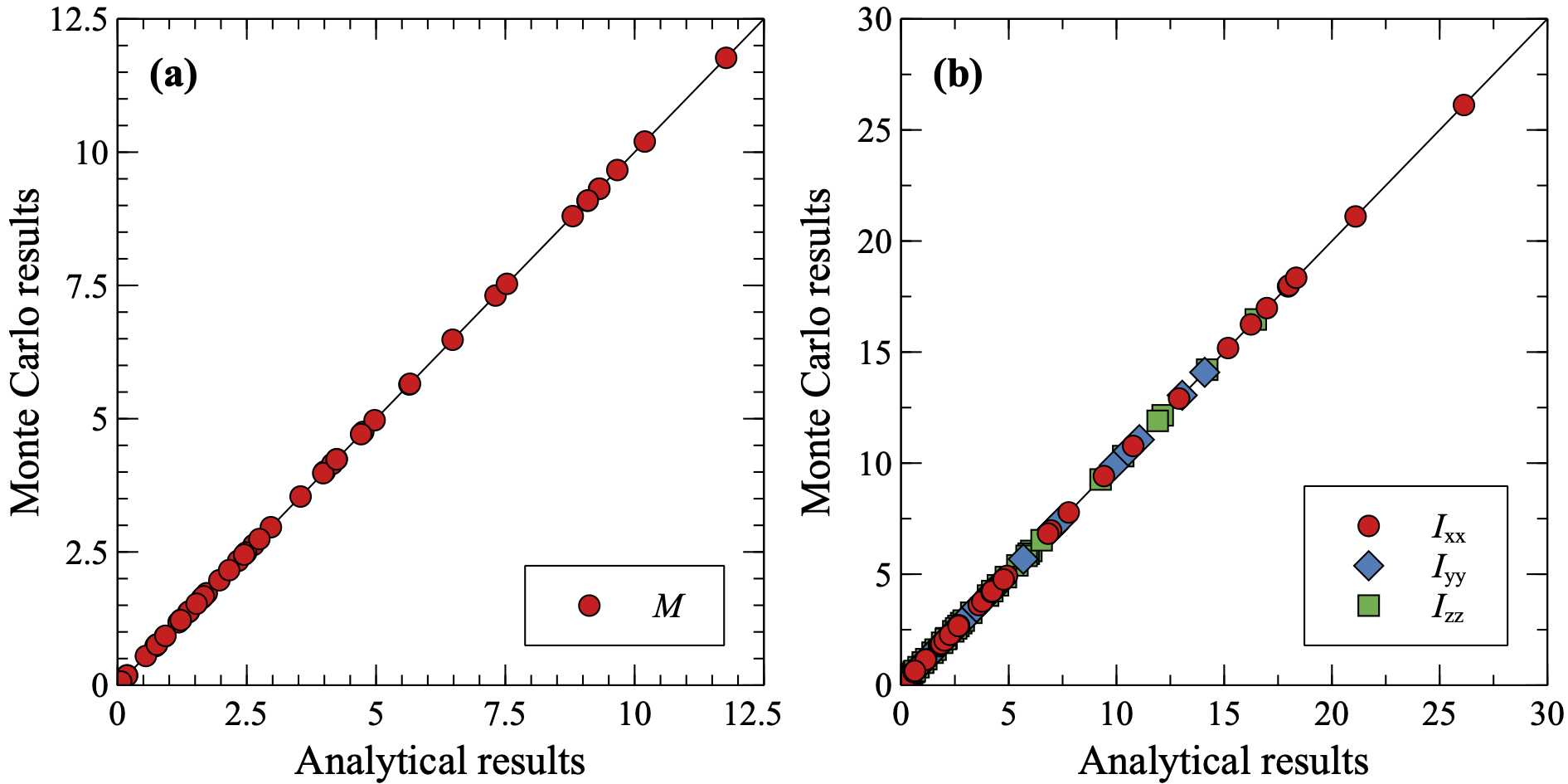
图 3.14 对于50个随机扩展超椭球，可以比较蒙特卡洛模拟和解析结果在以下方面的差异：(a) 质量和 (b) 主惯性矩。

可以使用蒙特卡洛方法根据给定函数 \(f(\mathbf{x})\) 在扩展超椭球的整个体积 \(V_{PS}\) 上进行数值积分，从而计算颗粒的属性（质量、质心和主惯性矩）。根据 [1] ，积分的计算可以按照以下方式进行：

\[\mathbf{P} = \int_{V_{PS}}f(\mathbf{x})\mathrm{d}v \simeq \frac{V_{box}}{N_p}\sum_{i=1}^{N_p}\xi(\mathbf{x}_i)f(\mathbf{x}_i)\]

在蒙特卡洛方法中，可以使用一组在包含扩展超椭球的长方体盒子内均匀分布的准随机点集 \(\{\mathbf{x}_i | i=1, \dots, N_p \}\) 进行数值积分。其中，\(N_p\) 是点的数量，\(V_{box}\) 是盒子的体积，\(\xi(\mathbf{x}_i)\) 是符号函数，如果 \(\mathbf{x}_i\) 在扩展超椭球内部，则其值为1，否则为0。函数 \(f(\mathbf{x}_i)\) 可以是 \(\rho\)、\(\rho\mathbf{x}_i\) 或 \(\rho||\mathbf{x}_i||^2\) ，分别对应积分 \(P=M\)、\(M\mathbf{x}_c\) 和 \(\mathbf{I}+M||\mathbf{x}_c||^2\) ，其中 \(\rho\) 是质量密度，\(M\) 、\(\mathbf{x}_c\) 和 \(\mathbf{I}\) 分别是质量、质心和惯性矩。蒙特卡洛方法得到的质量和主惯性矩在 图 3.14 中与解析解方程 (3.33) 和 (3.34) 的结果进行比较。其中， \(N_p=10^7\) ，\(\rho=1\) ，并且 \(r_x^+, r_x^-, r_y^+, r_y^-, r_z^+, r_z^-\) 在区间 \([0.01, 5.0]\) 内随机选择，而 \(\epsilon_1\) 和 \(\epsilon_2\) 在区间 \([0.1, 1.9]\) 内选择。蒙特卡洛方法和解析结果非常吻合。注：在构建惯性矩张量时，还需考虑非对角线上的量，但在上述局部坐标系中，这些值往往相对主对角线上的值小很多。

3.5.4. 运动方程

考虑两个笛卡尔坐标系：一个是全局坐标系 \(\hat{X}\hat{Y}\hat{Z}\) ，另一个是固定在质心处且轴与惯性主轴一致的局部坐标系 \(X^{'} Y^{'}Z^{'}\) ，使得惯性矩张量为对角矩阵。给定一个颗粒，它的平移和旋转分别由牛顿和欧拉方程控制，如下所示：

(3.35)\[\begin{split}F_{i}^{(b)} + f_{i}^{(d)}+ \sum_{c=1}^{N} F_{i}^{(c)}&= m\frac{\mathrm{d}v_i}{\mathrm{d}t} \\ T_{i}^{(d)} + \sum_{c=1}^{N} M^{(c)}_{i}&= I_i\frac{\mathrm{d}\omega_i}{\mathrm{d}t} - (I_j - I_k)\omega_j\omega_k\end{split}\]

其中，\(i, j, k\) 是连续的索引；\(m\) 是颗粒的质量；\(v_i\) 和 \(\omega_i\) 分别是颗粒质心的平移速度和绕质心的角速度；\(N\) 是接触的数量；\(F_i^{(c)}\) 是接触 \(c\) 处的接触力； \(F_i^{(b)}\) 是体力； \(I_i\) 是主惯性矩； \(M_i^{(c)}\) 是绕质心在接触 \(c\) 处的力矩； \(f_{i}^{(d)}\) 和 \(T_{i}^{(d)}\) 分别是阻尼力和阻尼力矩，它们被人为引入以促进系统中动能的耗散。非球颗粒的运动求解在 非球颗粒离散元模型 已有详细介绍。

在给定状态下，具有指定方向（或法向量） \(\mathbf{\hat{n}}\) 的颗粒的表面点（即全局坐标系中的支撑点）的全局坐标 \(\mathbf{\hat{x}}\) 可以通过以下方式给出：

(3.36)\[\mathbf{\hat{x}}= \mathbf{\hat{S}}(\mathbf{\hat{n}}) = \mathbf{R}S(\mathbf{R}^{-1}\mathbf{\hat{n}}) - \mathbf{x}_c + \mathbf{s}\]

其中， \(\mathbf{s}\) 是由牛顿方程求解得到的颗粒位置（即颗粒的质心）； \(\mathbf{R}\) 是从局部坐标系 \(X^{'} Y^{'}Z^{'}\) 到全局坐标系 \(\hat{X}\hat{Y}\hat{Z}\) 的旋转矩阵，即从欧拉方程求解得到的颗粒的旋转矩阵表示，并且 \(\mathbf{R}^{-1}\) 是其逆变换； \(S\) 是在局部坐标系 \(XYZ\) 中的支撑函数，在公式 (3.31) 中给出； \(\mathbf{x}_c\) 是在 \(XYZ\) 中的质心位置。

3.5.5. 接触及接触计算

对于扩展超椭球的一般接触检测（也称为碰撞检测），考虑两个连续的阶段，即粗略检测和精细检测阶段。对于粗略接触检测阶段，可采用与球包围盒结合的轴对齐包围盒（AABB）的扫除算法（ sweep and prune algorithm ） [2] 。在精细接触检测阶段，我们遵循常规接触概念 [5, 7] ，具体如下所述。

3.5.5.1. 接触几何与力学参量

给定 图 3.15 中显示的两个接触颗粒 A 和 B，根据共同法线概念，确定了每个颗粒表面上的两个接触点 \(\mathbf{p}^A\) 和 \(\mathbf{p}^B\)，其中颗粒表面在 \(\mathbf{p}^A\) 和 \(\mathbf{p}^B\) 处的外法线与接触法线 \(\mathbf{c}\) 共线。两个颗粒的嵌入可以通过接触点来定义，即 \(\mathbf{d}=\mathbf{p}^A-\mathbf{p}^B\) ，用于计算朝接触法线方向的斥力（即法向接触力 \(\mathbf{F}_{n}\) ）。垂直于嵌入且通过其中点（即 \(\frac{1}{2}(\mathbf{p}^A-\mathbf{p}^B)\) ）的平面被视为接触平面，在该平面上，切向接触力 \(\mathbf{F}_t\) （通常是滑动摩擦力）以增量方式作用，但受到库仑条件的约束。切向接触力 \(\mathbf{F}_t\) 和法向接触力 \(\mathbf{F}_n\) 的大小如下所示：

\[\begin{split}\begin{array}{ll} |\mathbf{F}_n| &= K_n |\mathbf{d}|\\ |\mathbf{F}_t| &= \min \{ |\mathbf{F}_t^{'} - K_t \Delta\mathbf{u}|, \mu|\mathbf{F}_n| \} \end{array}\end{split}\]

其中，\(K_n\) 和 \(K_t\) 分别是法向和切向接触刚度；\(\mathbf{F}_t^{'}\) 是上一个切向接触力，但需要旋转到当前接触平面上，当两个颗粒接触时，它被初始化为零；\(\Delta \mathbf{u}\) 是当前时间步长内接触平面上的相对位移；\(\mu\) 是滑动摩擦系数。

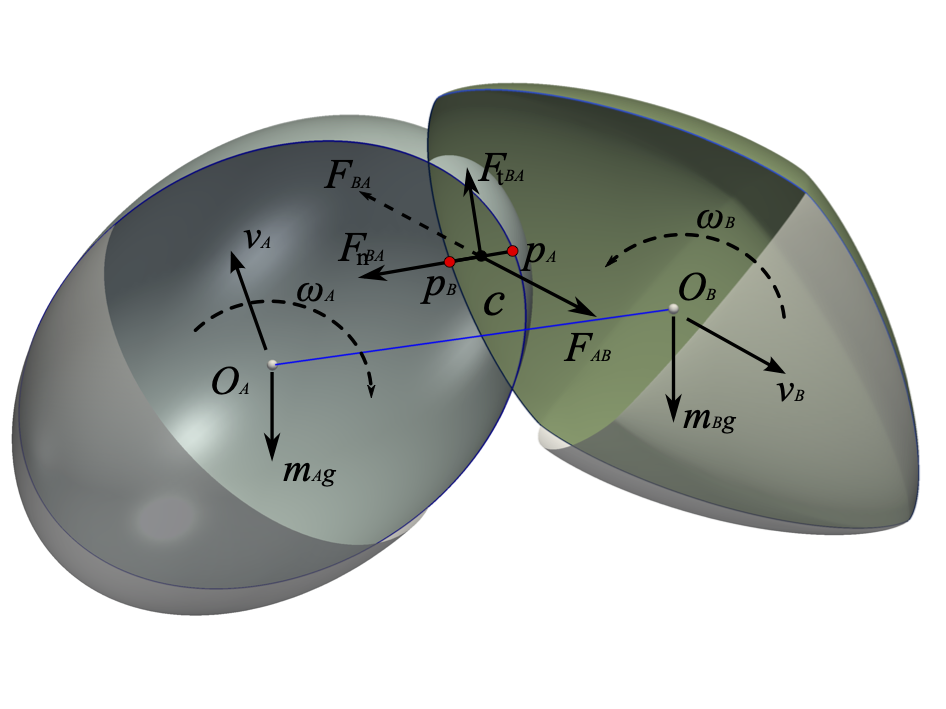
图 3.15 两个接触的颗粒(夸大了重叠)

3.5.5.2. 颗粒与墙接触

假设存在一个带有外法线 \(\mathbf{n}^B\) 的边界墙 B，通常认为颗粒与墙壁的接触发生在 \(\mathbf{n}^B\) 指向的一侧。根据共同法线概念，接触法线 \(\mathbf{c}\) 与 \(\mathbf{n}^B\) 的反方向相同，如 图 3.16 所示，因此给定颗粒 A 上的接触点 \(\mathbf{p}^A\) 可通过方程 (3.36) 中的全局支撑函数获得，表示为：

\[\mathbf{p}^A = \mathbf{\hat{S}}(-\mathbf{n}^B)\]

另一个接触点 \(\mathbf{p}^B\) 可以通过将 \(\mathbf{p}^A\) 投影到墙壁 B 上来轻松获得。因此，解决了嵌入 \(\mathbf{d} = \mathbf{p}^B - \mathbf{p}^A\) 和其他接触量。需要注意的是，正的 \(\mathbf{d}\cdot \mathbf{n}^B\) 对应于有效的接触（ 图 3.16 (a)），否则颗粒与墙壁的接触是虚拟的（ 图 3.16 (b)）。颗粒与墙壁接触检测的上述描述可以通过略微增加的计算成本轻松扩展到颗粒-面片对，只需检查 \(\mathbf{p}^B\) 是否位于面片内部即可。

图 3.16 颗粒与墙是否接触的二维示意

3.5.5.3. 颗粒间的接触

1. 最优化问题

通过引入共同法线概念 [5, 7] ，点 \(\mathbf{p}^A\) 处的外法线 \(\mathbf{n}^A\) 与接触法线 \(\mathbf{c}\) 具有共同的法线，而点 \(\mathbf{p}^B\) 处的外法线 \(\mathbf{n}^B\) 与 \(\mathbf{c}\) 的反方向相同，即：

(3.37)\[\mathbf{n}^A = -\mathbf{n}^B = \mathbf{c}\]

因此，考虑方程 (3.26) ，接触点可以表示为：

\[\mathbf{p}^A = \mathbf{\hat{S}}^A(\mathbf{c}), \quad{}\mathbf{p}^B = \mathbf{\hat{S}}^B(-\mathbf{c})\]

候选嵌入可以表示为：

\[\mathbf{d} = \mathbf{\hat{S}}^B(-\mathbf{c}) - \mathbf{\hat{S}}^A(\mathbf{c}) = -\mathbf{\hat{S}}_{A-B}(\mathbf{c})\]

其中，\(\mathbf{\hat{S}}_{A-B}\) 是颗粒 A 和 B 的闵可夫斯基差(Minkowski difference)的支撑函数。图 3.17 显示了任意两个凸形状 A 和 B 的闵可夫斯基差 \(C\) ，即 \(C = A - B = \{ a-b|a\in A, b\in B\}\) 。在此引入了一个有用的闵可夫斯基差引理 [6] ：如 图 3.17 (a) 所示，闵可夫斯基差 \(C\) 包围原点，表明颗粒 A 和 B 互相接触；反之亦然；而如果颗粒 A 和 B 没有交集，则闵可夫斯基差 \(C\) 不包围原点，反之亦然，如 图 3.17 (b) 所示。

图 3.17 两个任意凸形状颗粒 A 和 B 的闵可夫斯基差的二维示意：（a）表示存在接触，（b）表示没有接触。

寻找嵌入深度 \(||\mathbf{d}||\) 可以转化为以下带有接触法线 \(\mathbf{c}\) 作为参数的无约束优化问题：

(3.38)\[\underset{\mathbf{c}}{\mathrm{min}}||\mathbf{d}|| = \underset{\mathbf{c}}{\mathrm{min}}||\mathbf{\hat{S}}_{A-B}(\mathbf{c})||\]

等式 (3.28) 的相等性让我们可以使用两个有前景的迭代算法，即Levenberg-Marquardt（LM）算法 [5] 和Gilbert-Johnson-Keerthi（GJK）算法 [3] ，可以分别用于搜索嵌入深度。同时，这两个算法可以进行混合使用，以实现更稳健和高效的解决方案，详细说明见后。此外，候选嵌入 \(\mathbf{d}\) 可以被视为接触嵌入，一旦它与接触法线 \(\mathbf{c}\) 具有共同法线，即：

(3.39)\[\mathbf{d} \times \mathbf{c} = \mathbf{0}\]

2）LM 与 GJK混合

由于在颗粒系统的接触检测过程中存在密集的计算成本，需要一种高效的方法来解决优化问题。Levenberg-Marquardt（LM）算法 [5] 是一种常用于解决非线性最小二乘问题的方法，它是最陡下降法和牛顿-高斯法的组合。为了获得更好的LM算法性能，引入了参数空间的降维方案，具体如下所述。通过引入局部球坐标系，接触法线 \(\mathbf{c}\) 可以由两个角度 \(\alpha\) 和 \(\beta\) （以弧度表示）参数化，即：

(3.40)\[\mathbf{c}(\alpha, \beta) = \mathrm{cos}\alpha\mathrm{cos}\beta \mathbf{i}+ \mathrm{sin}\alpha\mathrm{cos}\beta \mathbf{j}+ \mathrm{sin}\beta \mathbf{k}\]

其中，\(\mathbf{i}, \mathbf{j}\) 和 \(\mathbf{k}\) 是全局笛卡尔坐标系的单位基向量。因此，优化问题变为：

(3.41)\[\underset{\alpha, \beta}{\mathrm{min}}||\mathbf{d}|| = \underset{\alpha, \beta}{\mathrm{min}}||\mathbf{\hat{S}}_{A-B}(\mathbf{c}(\alpha, \beta))||\]

在LM算法的实现中，为了实现更高的实现和计算效率，使用有限差分逼近来近似雅可比矩阵，而不是直接使用解析解。值得注意的是，当方程（ (3.28) 达到全局最小值时，方程（ (3.27) ）得到满足 [7] 。在解决优化问题时，将在每次迭代中检查以下条件：

\[\mathbf{d} \cdot \mathbf{c} > 0\]

如果这个条件为真，表示颗粒之间没有接触，参考 图 3.7 (b) 中的情况。因此，我们可以排除当前颗粒对的考虑，并终止优化过程。

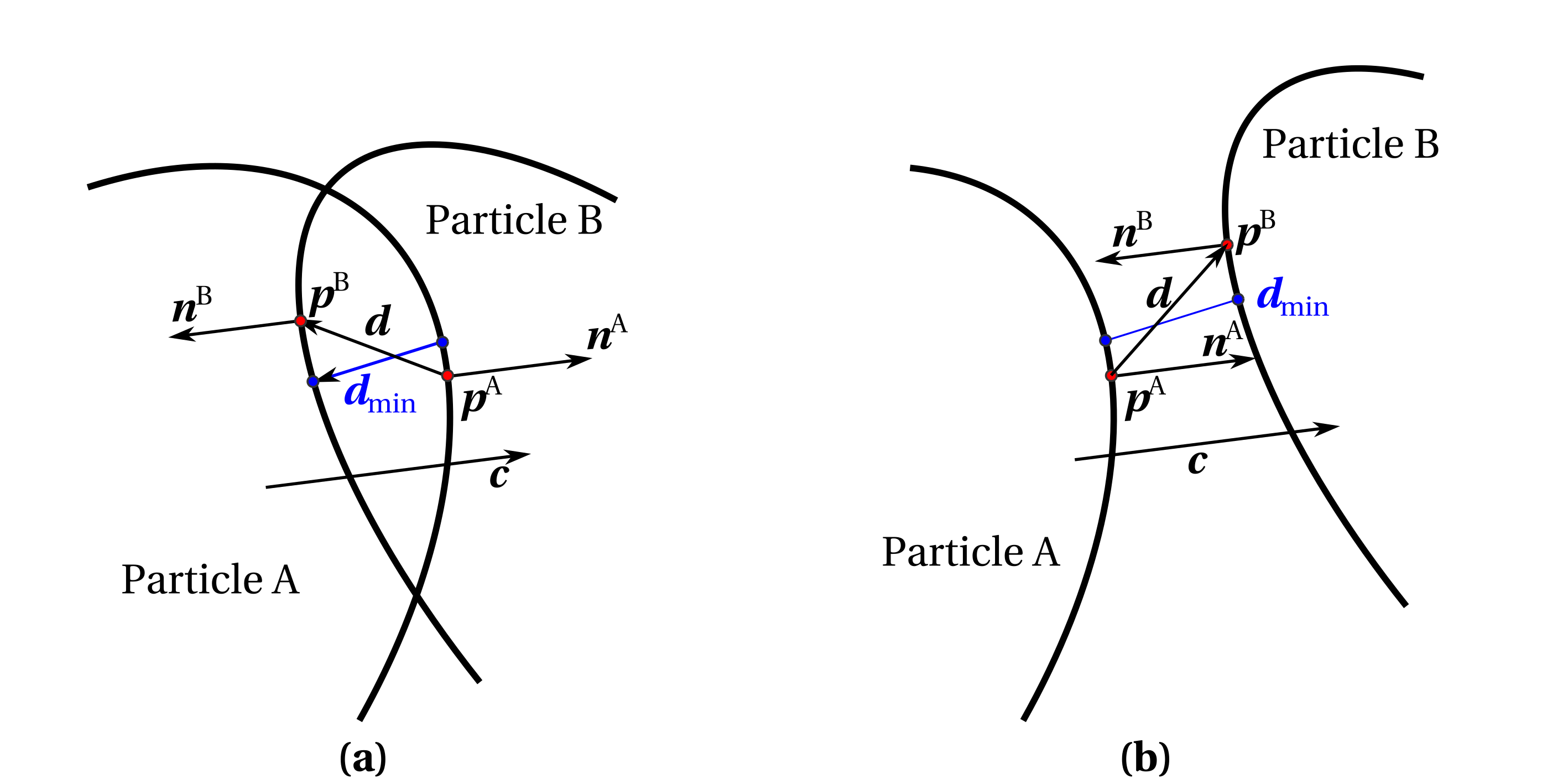
图 3.18 两个二维示意图分别表示了以下情况的优化求解：(a) 表示接触的颗粒对，(b) 表示非接触的颗粒对。

给出了两个重要的停止准则来指导LM优化的收敛，如下所示：

(3.42)\[\begin{split}\begin{aligned} |\mathbf{d} \cdot \mathbf{c}| > (1-\epsilon_{l}) ||\mathbf{d}||\\ \sqrt{(\Delta\alpha)^2+(\Delta\beta)^2} < \epsilon_m\end{aligned}\end{split}\]

其中，\(\Delta\alpha\) 和 \(\Delta\beta\) 是参数空间中的搜索步长；\(\epsilon_l\) 和 \(\epsilon_m\) 是控制精度的参数。通过LM算法搜索得到的嵌入深度 \(\mathbf{d}\) 更新为 \(|\mathbf{d}\cdot \mathbf{c}|\mathbf{c}\) 。

上述的LM优化具有良好的收敛性能。通常情况下，一般情况下只需要不到10次迭代就可以达到良好的收敛。然而，需要特别注意两种极端情况，其中LM优化可能失败或收敛速度显著变慢。一种情况是当从一个颗粒表面计算得到的接触点位于另一个颗粒的外部，另一种极端情况是LM算法以极小的步长收敛（例如，对于非常平坦的面对面接触，步长可能为 \(10^{-5}\) 弧度）。为了处理这两个可能在所提出的方法中遇到的问题，采用了Gilbert-Johnson-Keerthi（GJK）算法 [3] 。这就是所谓的LM和GJK算法的混合方法 [8] 。

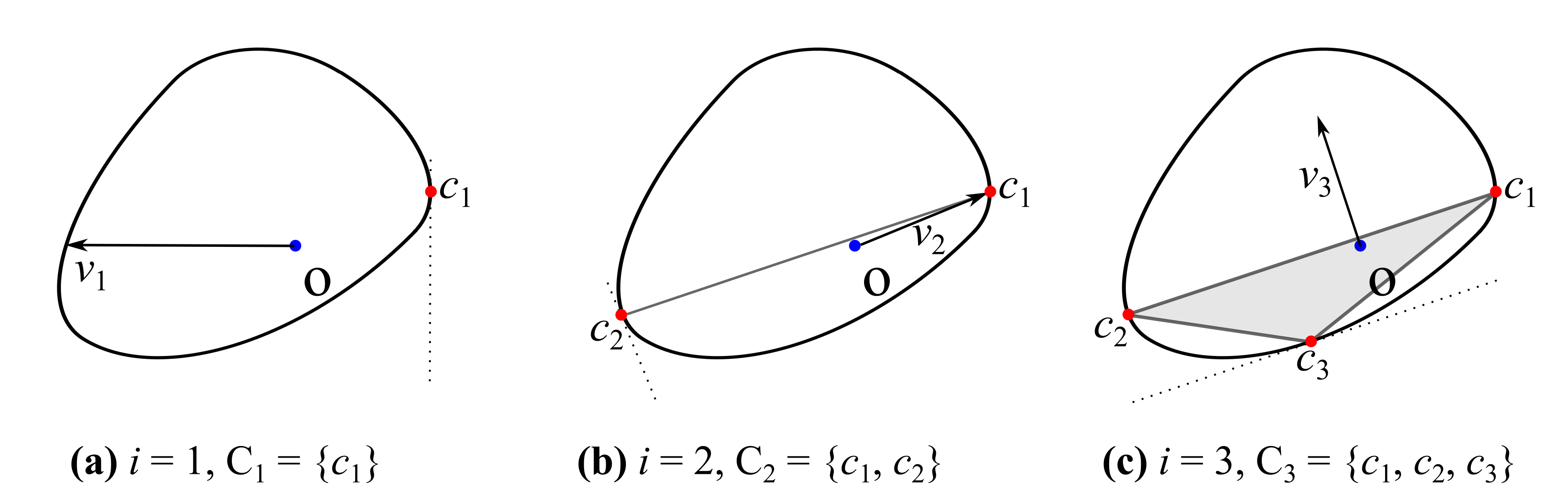
图 3.19 Minkowski差包含原点的GJK迭代二维示意

GJK算法是一种用于凸体接触检测的高效算法，广泛应用于计算机游戏和图形模拟中 [6] 。通常的GJK算法用于通过在给定两个物体的Minkowski差 \(C = A - B\) 中构造一系列单纯形来测试两个凸体是否相交。支撑函数和单纯形是GJK算法的关键组成部分。借助支撑函数，可以方便地计算给定搜索方向下的Minkowski差。单纯形最多有四个顶点位于Minkowski差 \(C\) 的边界上，它可以是一个点、一条线段、一个三角形（在二维情况下）或一个四面体（在三维情况下）。GJK算法的核心是迭代地在更新的单纯形上找到一个离原点更近的点。下面简要介绍GJK算法的工作原理。在每次迭代中，给定一个搜索方向 \(v_i\) ，可以通过支撑函数 \(\hat{S}_{A-B}(-v_i)\) 找到一个支撑点 \(c_i\) ，将其添加到先前的单纯形中以更新单纯形 \(C_i\) 。以 图 3.19 中的二维情况为例，第一次迭代中，给定任意的搜索方向 \(v_1\) ，得到初始单纯形 \(C_1=\{c_1\}\) ，如 图 3.19 (a) 所示；在第二次迭代中 \(i=2\) ，如 图 3.19 (b) 所示，搜索方向被更新为 \(v_2\) ，即给出先前单纯形 \(C_1\) 和原点之间最短距离的方向。然后得到一个更新后的单纯形 \(C_2=\{c_1, c_2\}\) 。迭代最终使得单纯形围绕着两个接触颗粒的原点，如 图 3.19 (c) 所示。通常情况下，GJK算法可以快速收敛，找到一个围绕原点的单纯形，即对于Minkowski差 \(C\) 。然而，GJK算法不能直接提供两个接触颗粒的最短距离。通常会采用一种称为扩展多面体算法（EPA）的算法 [6] ，以类似GJK的方式迭代逼近最短距离。然而，EPA算法的计算成本较高。

图 3.20 二维示意：(a) 用小圆盘（球）侵蚀形状 (b) 两侵蚀形状颗粒接触

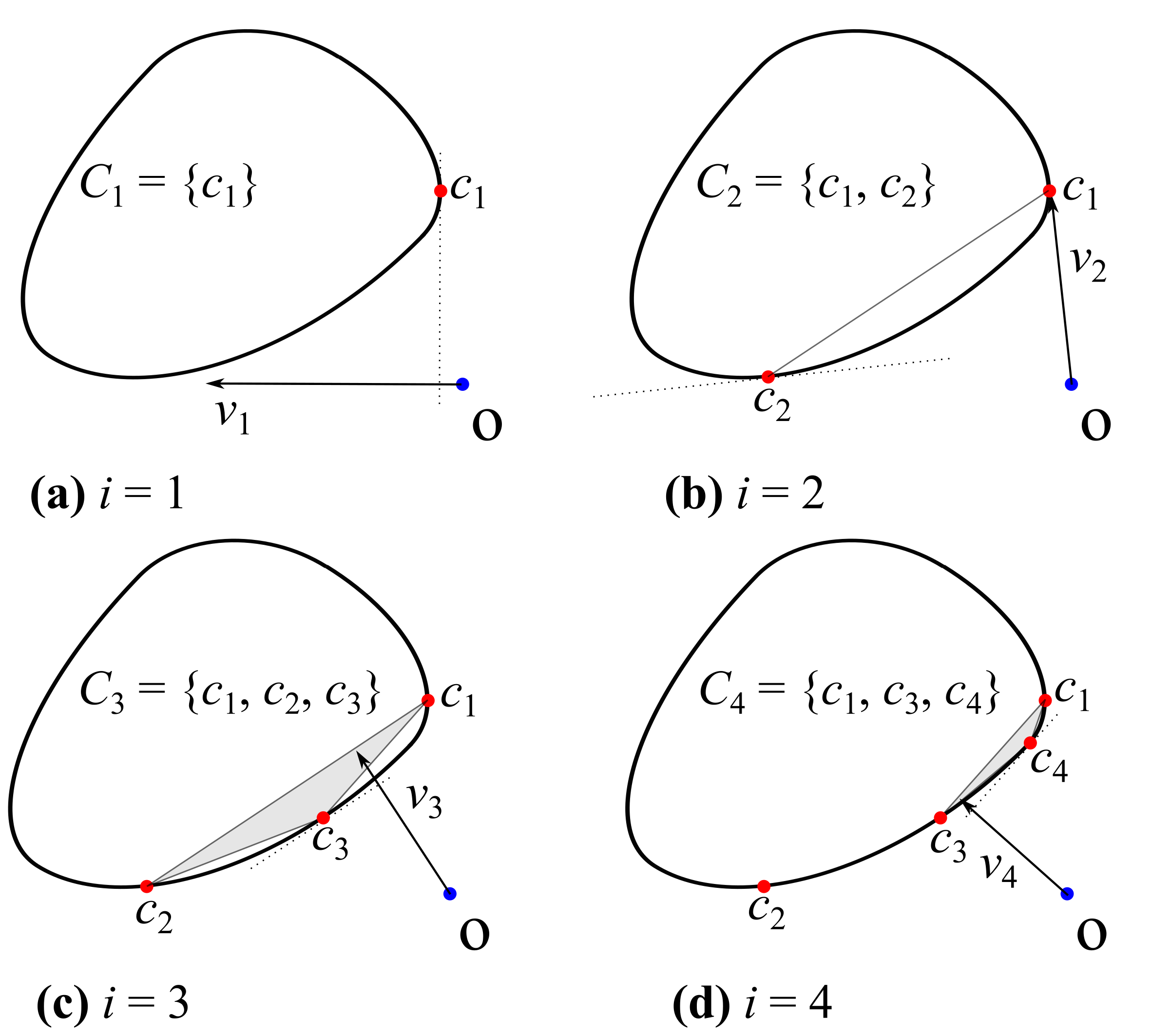
图 3.21 Minkowski差不包含原点的GJK迭代二维示意

根据一般DEM模拟中遇到的颗粒嵌入现象非常小的前提条件（DEM中的“软球”方法），我们提出了一种形状侵蚀方案来帮助计算嵌入深度。如 图 3.20 (a) 所示，颗粒形状沿着内部法线向内侵蚀一小段距离 \(\delta_r\) ，使得两个接触颗粒的侵蚀形状分离，如 图 3.20 (b) 所示。通过这种方式，可以使用GJK算法计算两个非接触颗粒的嵌入深度 \(d^{'}\) ，与对接触颗粒的计算方式类似（参见 图 3.21 ）。GJK算法在达到一定精度时终止，即

(3.43)\[||\mathbf{v}_i||^2 - \mathbf{v}_i \cdot \mathbf{c}_i < \epsilon_c||\mathbf{v}_i||^2\]

其中 \(\mathbf{v}_i\) 是单纯形 \(C_i\) 中离原点最近的点。因此，两个侵蚀颗粒表面上最接近的点 \(\mathbf{p}^{A^{'}}\) 和 \(\mathbf{p}^{B^{'}}\) 可以得到，而接触点 \(\mathbf{p}^{A}\) 和 \(\mathbf{p}^{B}\) 则可以表示为：

\[\mathbf{p}^{A} = \mathbf{p}^{A^{'}} + \delta_r^A\mathbf{c}, \quad{}\mathbf{p}^{B} = \mathbf{p}^{B^{'}} - \delta_r^B\mathbf{c}\]

与

(3.44)\[\mathbf{c}=-\frac{\mathbf{v}}{||\mathbf{v}||}\]

其中 \(\delta_r^A\) 和 \(\delta_r^B\) 分别是两个颗粒 A 和 B 的侵蚀距离；\(\mathbf{c}\) 是接触法线；\(\mathbf{v}\) 是最新单纯形中离原点最近的点。

通过方程 (3.40) 和 (3.44) ，可以轻松地在LM中将参数 \(\alpha\) 和 \(\beta\) 与GJK中的参数 \(\mathbf{v}\) 进行切换，从而实现这两种算法的无缝组合。此外，在DEM模拟过程中，可以缓存当前帧的接触法线 \(\mathbf{c}\) ，并将其作为下一帧的初始猜测值，从而节省计算时间。

3.5.6. 参考文献

[1]

Fernando Alonso-Marroquín and Yucang Wang. An efficient algorithm for granular dynamics simulations with complex-shaped objects. Granular Matter, 11(5):317–329, 2009.

[2]

Gino van den Bergen. Efficient collision detection of complex deformable models using aabb trees. Journal of Graphics Tools, 2(4):1–13, 1997.

[3] (1,2)

Elmer G Gilbert, Daniel W Johnson, and S Sathiya Keerthi. A fast procedure for computing the distance between complex objects in three-dimensional space. IEEE Journal on Robotics and Automation, 4(2):193–203, 1988.

[4] (1,2)

KL Johnson. Contact Mechanics. Cambridge University Press, London, 1985.

[5] (1,2)

Manolis IA Lourakis. A brief description of the levenberg-marquardt algorithm implemented by levmar. Foundation of Research and Technology, 4(1):1–6, 2005.

[6] (1,2,3)

Gino Van Den Bergen. Collision detection in interactive 3D environments. CRC Press, 2003.

[7] (1,2,3)

Christian Wellmann, Claudia Lillie, and Peter Wriggers. A contact detection algorithm for superellipsoids based on the common-normal concept. Engineering Computations, 25(5):432–442, 2008.

[8] (1,2)

Shiwei Zhao and Jidong Zhao. A poly-superellipsoid-based approach on particle morphology for DEM modeling of granular media. International Journal for Numerical and Analytical Methods in Geomechanics, 43(13):2147–2169, 2019.