4.1. MPM vs FEM¶

MPM隶属于无网格法或者弱网格依赖方法。MPM主要包括物质点和背景网格两部分，物质点携带所有状态信息，例如动量、应力及应变等，而背景网格仅在求解映射中发挥作用，本身并不携带任何状态信息。与经典的有网格法有限元法 (FEM) 相比，MPM可被视为高斯点可自由移动的特殊FEM方法。

传统的FEM求解过程如下 (Python 伪代码)：

列表 4.1 FEM求解流程¶

import fem  # 总刚度矩阵, K; 节点位移, u; 增量位移, du; 总荷载, b;
for i in range(steps):
    #组装局部刚度矩阵
    for ele in fem.elements:
        # B为位移-应变协同矩阵, D为等效雅可比
        ele.K = ele.BTDB()
        # 单元到总刚的坐标映射矩阵
        trsf = ele.Transformation()
        # 组装总刚度矩阵
        K += trsf.T * ele.K * trsf
        # 应力加载
        stress = stress + D * (BT * du)
        b += trsf.T * stress
    # 加载外力边界
    for nd in fem.nodes()
        b += nd.extf()
    # 边界条件，以拉格朗日乘子算法为例
    # lambda 为拉格朗日乘子, O为零矩阵
    # bclhs 为位移约束条件左侧系数矩阵； bcrhs 为位移约束条件右侧系数矩阵
    K = [[K, lambda * bclhs], [(lambda * bclhs).T, O]]
    du = [[du], [lambda]]; b = [[b], bcrhs]
    # 求解，直接求解: QR, PLU, CHOLESKY；迭代求解：PCG
    du = fem.Solve(); u += du
    # 检测是否收敛
    if(fem.checkConverge()): break

代码高亮部分与FEM网格畸变的显著相关，当材料求解域发生较大变形，尤其是剪切变形时，高斯点与节点映射矩阵会出现奇异，进而导致计算不收敛。

MPM针对此数值不稳定性做出的改善如下：

列表 4.2 MPM求解流程¶

import mpm
#物质点位移, u; 质量，m； 速度, v;
#物质点体积，vol；应力，stress
u, v, m, stress = mpm.mps()
#节点质量，node_m；速度，node_v；动量，node_mv；力，node_f
node_m, node_v, node_mv, node_f = mpm.nds()

for i in range(steps):
    #更新映射函数sf；映射梯度函数dsf
    sf = sf(u); dsf = dsf(u)
    #P2G: 物质点向节点映射映射动量、质量
    node_m = sf * m
    node_mv = sf * m * v; node_v = node_mv / node_m
    #G2P: 节点向物质点映射速度梯度gradv；F为变形梯度
    gradv = dsf * node_v; dF = e^(gradv * dt) * F
    vol = det(dF) * vol
    stress = stress(D, dF)
    #P2G: 物质点向节点映射应力
    node_f = vol * dsf * stress
    #G2G: 节点积分
    node_v += node_f * dt / node_m
    #G2P: 节点向物质点映射速度
    v = node_v * sf
    u += v * dt

高亮部分为MPM动态更新的节点与物质点映射函数；该灵活的映射关系以损失一定的计算精度为代价，为MPM换取了求解大变形问题更为稳定的收敛性。

备注

尽管FEM与MPM都会在计算中更新形函数或其偏导，但相较FEM，MPM物质点与节点的映射关系是非恒定的。

4.2. MPM 离散与迭代格式¶

4.2.1. 插值形函数¶

MPM求解域的节点与物质点构型参见图 4.1。图中浅蓝色区域为求解域，深蓝色点为离散表征材料的物质点，红色点为节点。物质点与节点的插值过程如红色箭头与黄色区域所示，物质点与所处其插值形函数范围的节点发生映射。

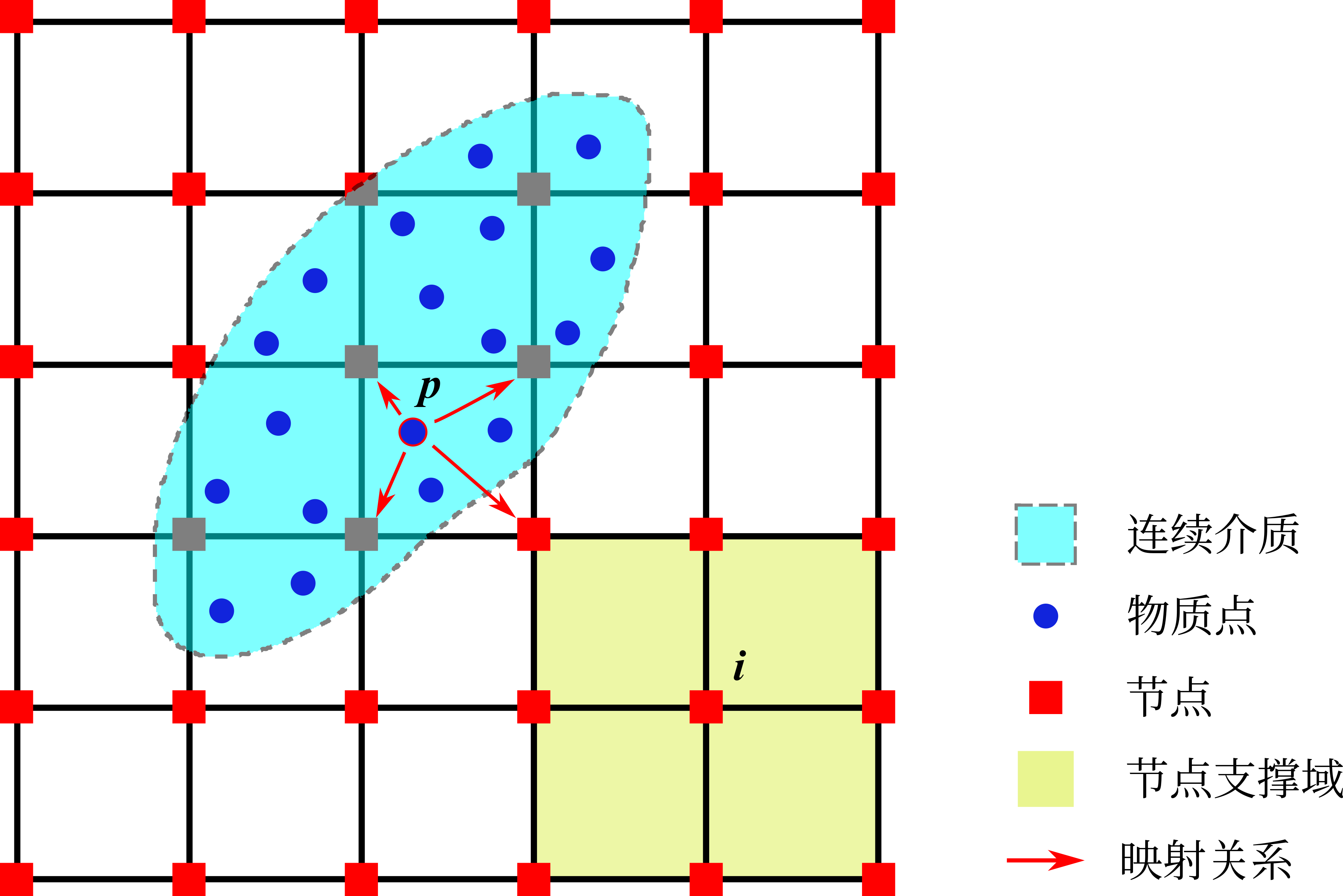
../_images/mpmdomain.png — 图 4.1 物质点法拉格朗日及欧拉描述示意图¶

MPM与FEM遵循相同的动量方程强形式，

(4.1)¶\[\rho \mathbf{a} = \nabla \cdot \mathbf{\sigma} + \rho \mathbf{b}\]

但MPM具有不同的离散形式，

(4.2)¶\[\begin{split}\mathbf{f}_{i}^{(n)} &= \mathbf{f}_{i, ext}^{(n)} + \mathbf{f}_{i, int}^{(n)} \\ \mathbf{p}_{i}^{(n)} &= \sum_{p}\mathbf{p}_{p}^{(n)}S_{ip}^{(n)} \\ \mathbf{m}_{i}^{(n)} &= \sum_{p}\mathbf{m}_{p}^{(n)}S_{ip}^{(n)} \\ \mathbf{p}_{i}^{(n+1)} &= \mathbf{p}_{i}^{(n)} + \mathbf{f}_{i}^{(n)} \Delta t\end{split}\]

MPM对质量、动量以及接触力的离散基于插值形函数，经典形函数称为线性形函数，这也是FEM的节点与高斯点的映射函数格式。MPM2D 不仅支持线性形函数，同时支持更为高阶的 GIMP [1] 和 CPDI [2] 函数，用以降低物质点穿越网格导致的信息丢失。

4.2.2. 迭代格式¶

以GIMP为例，形函数及其偏导的计算依据如下公式，

(4.3)¶\[\begin{split}S_{ip} &= \frac{1}{V_{p}}\int_{\Omega_{p} \cap \Omega} \chi_{p}(\textbf{x})N_{i}(\textbf{x})dV \\ G_{ip} &= \frac{1}{V_{p}}\int_{\Omega_{p} \cap \Omega} \chi_{p}(\textbf{x})\nabla N_{i}(\textbf{x})dV\end{split}\]

Footnotes

物质点与节点在求解不同阶段进行不同方向以及不同 状态量 的映射，

求解阶段

映射状态量

P2G

质量，动量

USF:G2P

速度梯度

USF

应变及应力

P2G

外力及内力

G2P

速度及加速度

G2G

牛顿积分

USL:G2P

速度梯度

USL

应变及应力

求解阶段	映射状态量
`P2G`	`质量，动量`
`USF:G2P`	`速度梯度`
`USF`	`应变及应力`
`P2G`	`外力及内力`
`G2P`	`速度及加速度`
`G2G`	`牛顿积分`
`USL:G2P`	`速度梯度`
`USL`	`应变及应力`

P为Particle缩写，G为Grid缩写。P2G表示物质点向节点的映射，G2P表示节点向物质点的映射。P2P和G2G各自表示物质点或节点自身的状态量更新。图 4.2 给出了P2G，G2G，G2P以及P2P的映射过程。

../_images/mpmiter.png — 图 4.2 物质点法迭代流程¶

当物质点与节点自由度相差较大时，MPM的G2P阶段的速度梯度映射会显著提高应变和应力更新的求解误差。USF (Update Stress First) 和USL (Update Stress Last) 迭代格式分别在G2P阶段前后完成应力和应变更新，用以降低映射误差。

4.3. MPM多物理场求解¶

4.3.1. 热求解¶

MPM2D 热力学求解的离散形式如下，

(4.4)¶\[\begin{split}C_{IJ} &= \sum_pm_pc_p\phi_{Ip}N_{Jp} \\ Q_I^{ext} &= \sum_p V_p\phi_{Ip}(Q_{tp} + L\rho_s\theta_{sp,t})+ \sum_p\bar{q}_ph^{-1}\phi_{Ip} \\ Q_I^{int} &= \sum_pV_p\phi_{Ip,i}k_{pij}T_{p,j} \\ \sum_JC_{IJ}T_{J,t} &= Q_I^{ext} + Q_I^{int}\end{split}\]

与力学求解类似，热的求解同样遵循P2G2P顺序，但由于热力学方程的温度偏导为二阶，所以有两次P2G阶段分别映射温度及 热通量 :

P2G: 物质点向节点映射温度场
G2P: 节点向物质点映射温度场梯度
P2G: 物质点向节点映射热通量
G2G: 节点更新温度
G2P：节点向物质点映射温度

注意

MPM2D 实现了热力耦合求解，在其内部力与热求解器采用 独立迭代-信息映射-独立迭代 的模式完成耦合。在非信息映射阶段，热与力可并行完成各自迭代过程。MPM2D 信息映射 阶段可通过边界条件以及材料本构完成热与力的耦合。MPM2D 支持热力混合边界，同时支持连续介质本构模型以及DEM RVE多尺度模型的热力响应，包括热力应变、热力张量以及相变。详细请参见相变及多尺度章节。

4.3.2. 相变求解¶

MPM2D 的热力-相变求解基于固相-冰相-液相混合理论，假定混合介质饱和度为1，同时不考虑液相相对流动以及热传导和对流过程。MPM2D 在宏观尺度通过热力学框架完成液相和冰相冻融循环模拟，在细观尺度为连续介质本构或DEM RVE多尺度模型提供材料热力-相变响应接口。

对于图 4.3 中所示的混合介质，固相和液相等效热学状态量由下式给出，

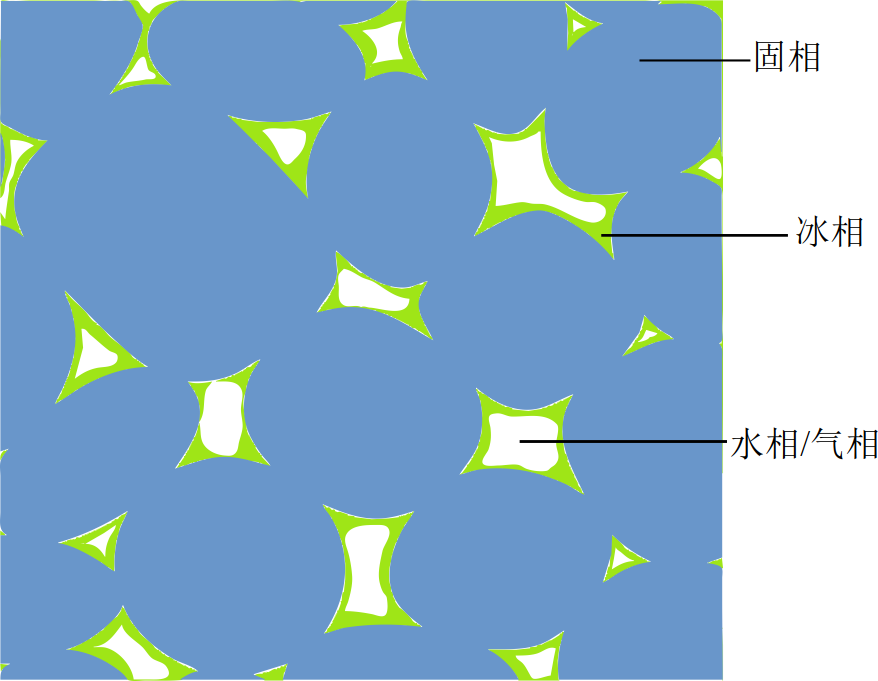
../_images/phasetransition.png — 图 4.3 包含固相、液相和冰相的混合介质¶

(4.5)¶\[\begin{split}\rho c &= \rho_fc_f\theta_f+\rho_sc_s\theta_s+\rho_gc_g\theta_g \\ k &= k_g^{\theta_g}k_f^{\theta_f}k_s^{\theta_s} \\\end{split}\]

固相和液相孔隙比控制方程有，

(4.6)¶\[\rho_f\theta_f - \rho_s\theta_s = 0\]

液相和冰相考虑未冻水的孔隙比控制方程有，

(4.7)¶\[\begin{split}\theta_s &= n - \frac{\rho_g}{\rho_f}(1-n)w \\ w &= \bar{w} + (w_0-\bar{w})e^{a(T-T_0)} \\ \theta_{s,T} &= - \frac{\rho_g}{\rho_f}(1-n)a(w_0-\bar{w})e^{a(T-T_0)}\end{split}\]

相变潜热控制方程有，

(4.8)¶\[\begin{split}\rho c T_{,t} + q_{i,i} &= Q_t + L\rho_{s}\theta_{s,t} \\ \theta_{s,t} &= - \frac{k_{pij}T_{p,j}}{L\rho_s} \\\end{split}\]

最终得到相变在热求解中的等效状态量，

(4.9)¶\[\begin{split}C_I &= \sum_pm_p(c_p-\frac{\rho_sL}{\rho_p}\theta_{sp,T})\phi_{Ip} \\ Q_I^{ext} &= \sum_p V_p\phi_{Ip}Q_{tp} + \sum_p\bar{q}_ph^{-1}\phi_{Ip} \\ \theta_s^{t+\Delta t} &= n - \frac{\rho_g}{\rho_f}(1-n)(\bar{w} + (w_0-\bar{w})e^{a(T_{p}^{t+\Delta t}-T_0)})\end{split}\]

相变与热求解的耦合公式 (4.9) 体现了相变潜热对材料热力场的额外贡献，进而将材料热力响应与固液相孔隙比转化联系起来。

若要进一步表征相变对材料应力-应变关系的关系，则需考虑材料初始状态固相孔隙率，相变过程中未冻水消散速率以及相变对材料塑性因子的影响。MPM2D 的DEM RVE多尺度模块综合考虑以上因素，为多尺度和多物理场复杂初值和边值问题的求解提供了可能，详情参见多尺度章节。

4.3.3. 接触求解¶

MPM2D 支持MPM经典的基于网格的多体接触算法。MPM网格接触引擎利用节点速度场判别多体接触与否：

(4.10)¶\[\begin{split}\mathbf{v}_{c} &= \frac{m_{a}\mathbf{v}_{a} + m_{b}\mathbf{v}_{b} }{m_{a} + m_{b}} \\ -&m_{a}(\mathbf{v}_{a} - \mathbf{v}_{c}) \cdot \mathbf{n} < 0\end{split}\]

警告

传统的接触检测算法在接触法向确定方面具有较大任意性；若引入GIMP形函数，材料可能发生提前接触。

MPM2D 同时提供了更为灵活的DEM驱动的多体接触引擎如图 4.4 所示，DEM接触引擎分为：

刚体-非刚体接触

非刚体-非刚体接触

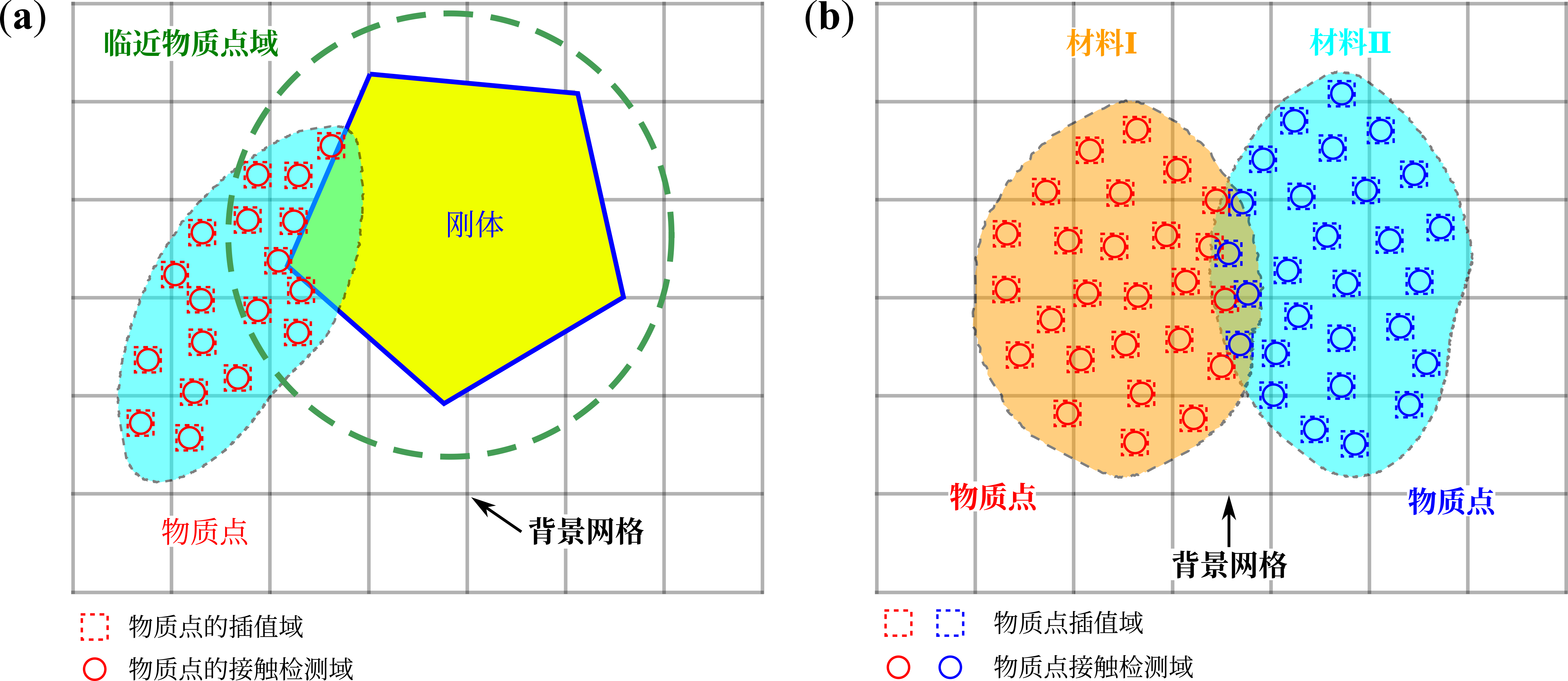
../_images/contacttypes.png — 图 4.4 **MPM2D** 接触类型：(a) 刚体-非刚体；(b) 非刚体-非刚体¶

刚性物质点 或者 刚性块 多用于边界条件的施加，在此过程中接触算法仅更新非刚体物质点的动量信息。非刚体-非刚体 接触算法中不涉及刚性物质点，所有与接触相关的物质点都会进行动量的更新。

不同材料物质点的接触力由 嵌入深度 和速度决定 (图 4.5)，

(4.11)¶\[\begin{split}\mathbf{f}_{n}^{n+1} &= k_{n}\delta \cdot \mathbf{n} \\ \mathbf{f}_{t}^{n+1} &= \min(\mathbf{f}_{t}^{n} + \Delta \mathbf{f}_{t}, \mu ||\mathbf{f}_{n}^{n+1}||) \\ \Delta \mathbf{f}_{t} &= k_{t}\Delta \mathbf{u} \\ \Delta \mathbf{u} &= (\mathbf{v}_{A} - \mathbf{v}_{B})\Delta t - [(\mathbf{v}_{A} - \mathbf{v}_{B}) \cdot \mathbf{n}]\mathbf{n}\Delta t\end{split}\]

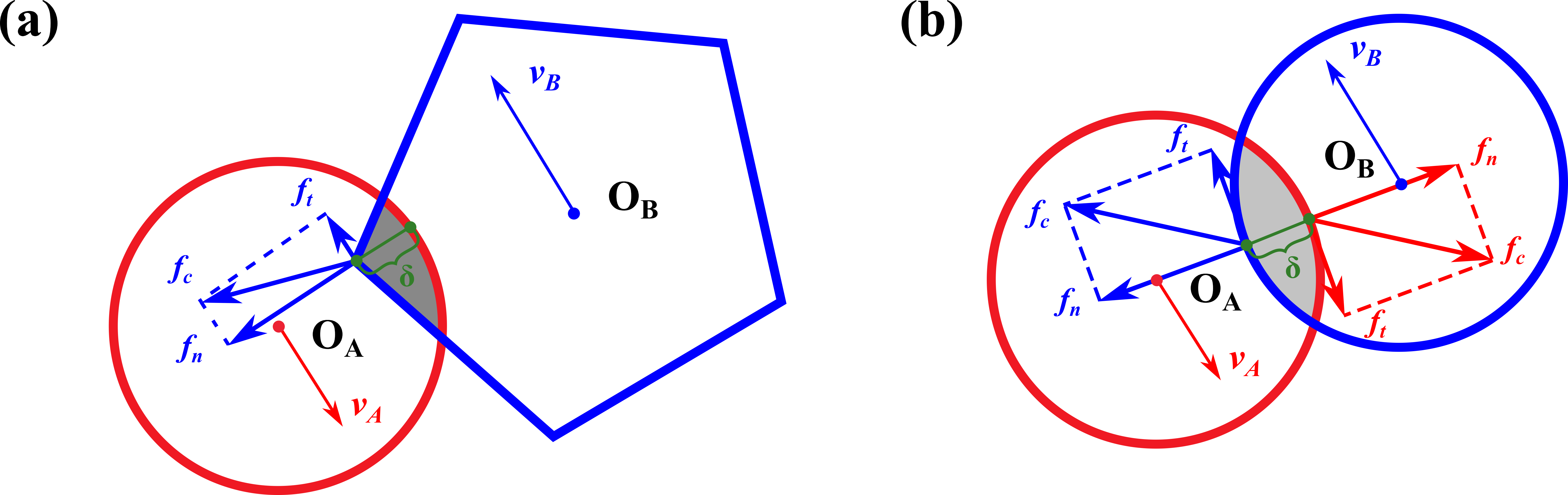
../_images/detection.png — 图 4.5 **MPM2D** DEM接触的力-位移定律¶

物质点或刚体的形状和位置确定了接触的法向，灰色的嵌入面积或绿色的嵌入深度决定了 法向接触力 的大小，接触物体的相对速度决定了 切向接触力 的大小。

接触力的施加参见图 4.6，图中给出了以面力方式施加接触力的示意图，虚线表示的uGIMP插值域在节点帮助下完成物质点的接触力积分及施加。

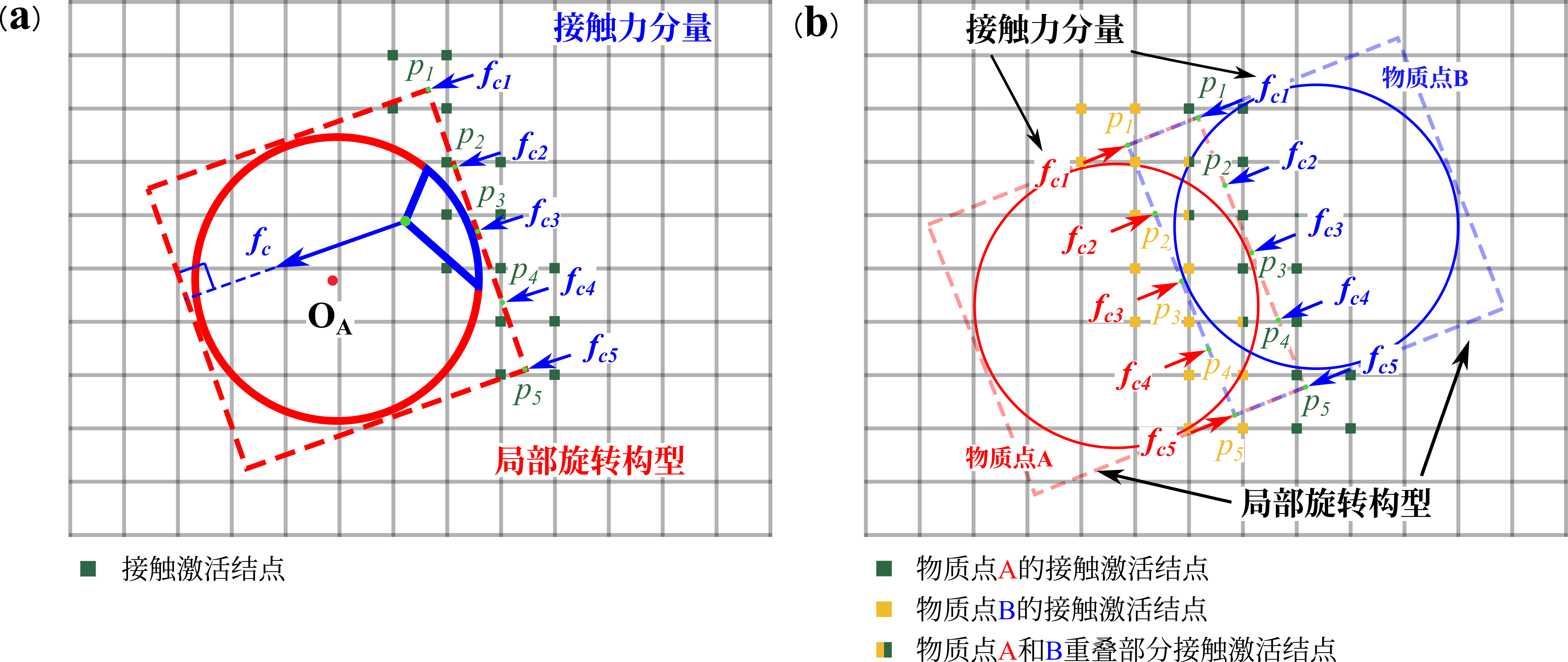
../_images/forceimposition.png — 图 4.6 **MPM2D** DEM接触力施加：(a) 刚体-非刚体；(b) 非刚体-非刚体¶