3.3. 多面体离散元模型¶
3.3.1. 多面体颗粒¶
在代数几何学中,我们可以定义一个N面凸多面体为由N个包围面 \(\{p_i|i=1,\dots,N\}\) 构成的凸包围集,即一组不等式集:
其中 \((a_i,b_i,c_i)\) 是第 \(i\) 个包围平面 \(p_i\) 的法向量, \(d_i\) 是 \(p_i\) 到原点的距离。
多面体的基本几何参量(如表面积、体积、质心坐标、惯性矩等)可通过经典的计算几何算法求得。比如,在求解多面体的体积时,可先将多面体剖分成一系列的四面体,再对这些四面体的体积求和即可。其它几何参量的求解思路类似,此处从略。
3.3.2. 接触检测¶
如图 图 3.3 为两相互接触的多面体颗粒,其中夸大显示了颗粒间的重叠部分。多面体颗粒间的接触检测已经得到了很多关注,尤其在计算几何领域。给定一对可能相互接触的多面体颗粒,记为 \(P_A\) 和 \(P_B\) ,两多面体是否接触等价为两凸集是否存在交集。
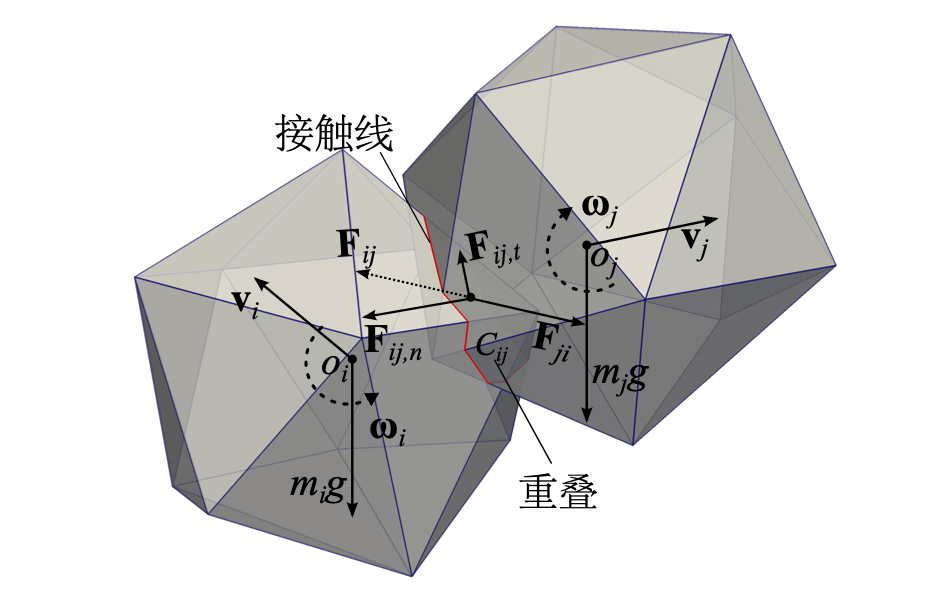
图 3.3 两多面体颗粒间接触的三维示意图¶
多面体颗粒间的接触检测要比球形颗粒间的接触检测复杂得多。对于球形颗粒,根据其位置和半径即可快速获得两个颗粒的重叠,见式 (3.12) 。然而,对于多面体颗粒,重叠区域(参见 图 3.3 是不规则的,并且它具有多个接触点(例如在面面或面边接触处)。因此,在大多数情况下,计算两个多面体颗粒的重叠是比较耗时的。由于在每个时间步长中需要对大量的颗粒进行相互接触检测,我们可以把接触检测分成两个过程(近似接触检测和精确检测)来减少计算时间。
为了加速接触检测过程,我们首先采用轴对齐包围盒(AABB)算法进行粗略地接触检测。轴对齐包围盒算法简介参见本章上一小节。对于使用AABB算法不能排除的颗粒对,需要执行进一步的精确检测,从而判断两颗粒之间是否存在接触。在这种情况下,我们利用分离轴(或分离面)算法进行进一步接触检测。设想存在一个分离面 \(S=\{(x,y,z) | a_sx + b_sy+ c_sz = d_s \}\) 使得来自多面体 \(P_\mathrm{A}\) 和 \(P_\mathrm{B}\) 的所有顶点分别在分离面的两侧。有三类平面可作为候选分离面 [3] :
多面体 \(P_\mathrm{A}\) 的包围面;
多面体 \(P_\mathrm{B}\) 的包围面;
分别由多面体 \(P_\mathrm{A}\) 的一条边和多面体 \(P_\mathrm{B}\) 的一条边构成的平面。
如果能找到这样一个分离面,那么两多面体颗粒间不存在接触,否则,两多面体颗粒相互接触。对于两相互接触的多面体颗粒,需要进一步计算接触处的相关几何量,如接触重叠量(嵌入深度或体积)、接触法向等,相关过程见下一小节。
3.3.3. 接触计算¶
在每一接触处,需要计算相应的几何参量,如接触重叠量、接触中心以及接触法切向等。其中,接触重叠量可以是接触嵌入深度或接触重叠体积,而本模型采用接触重叠体积,这是因为下文具体的接触计算方法可以方便地给出接触重叠体积。值得指出的是,颗粒与墙(平面)的接触是颗粒间接触的退化形式,因此,此处重点介绍颗粒间的接触计算。
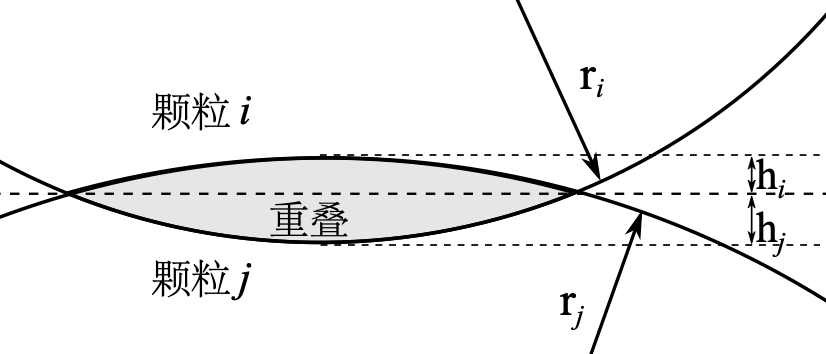
图 3.4 球形颗粒间的接触¶
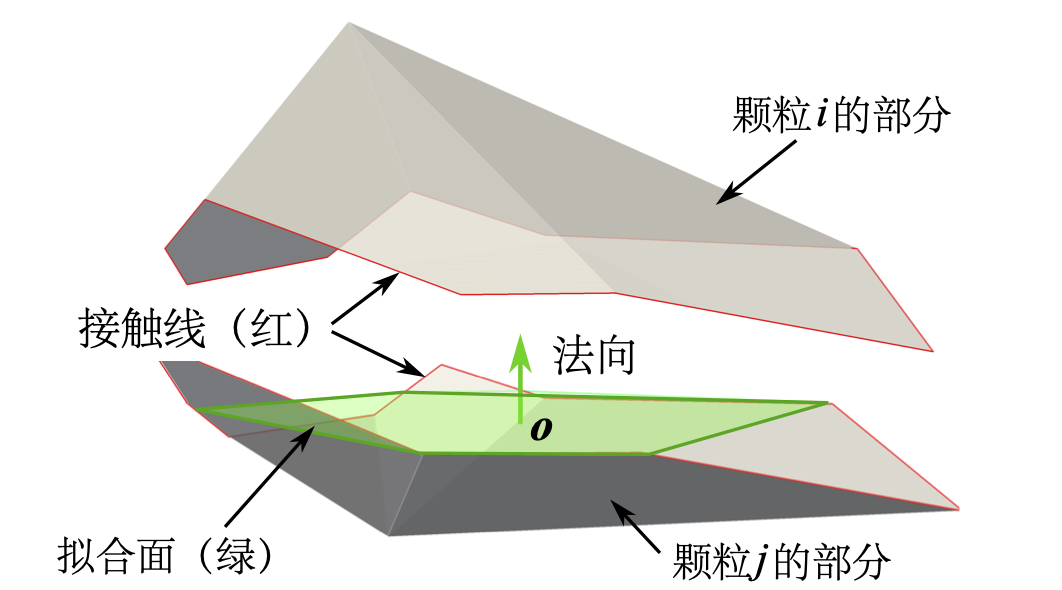
图 3.5 多面体颗粒间的接触(为便于可视化,相交多面体由接触线剖分为两部分)¶
对于球形颗粒,接触重叠体积(见 图 3.4 可通过简单的几何计算求得,如下:
式中, \(r_i\) (或 \(r_j\) )和 \(h_i\) (或 \(h_j\) )分别是第 \(i\) (或 \(j\) )个颗粒的半径和球冠高度。其他几何参数也可以通过显式表达式给出,此处从略。
相比之下,对于多面体颗粒,颗粒间的重叠区域往往是不规则多面体,并没有明确的统一理论表达式来计算相应的几何参量。学者相继提出和发展了多种针对多面体颗粒的精确接触检测的算法,比如,公共平面(CP)算法 [2] 、快速公共平面(FCP)算法 [10] 以及内部潜在颗粒法 [1] 。这些方法能够计算多面体接触的嵌入深度,但具体算法的实现比较繁琐。因此,我们利用一种基于所谓的对偶理论 [4, 7] 的方法来求解重叠多面体。感兴趣的读者可在文献 [3, 4, 7] 中找到关于这种方法的更多细节,在此只给出主要的操作步骤,如下:
全局坐标系向局部坐标系转换。局部坐标系的原点(以下简称为新原点)需要设置在接触重叠多面体内部。对于一个新的接触,由于在上一时步中并不存在相关信息,需要遍历两个接触多面体的所有边和面直到找到一个属于重叠的点为止;通过将该点向接触重叠内部移动一小距离便可得到新原点。对于一个已经存在的接触,来自上一时步的接触点可作为新原点。
由模型空间向对偶空间映射。模型空间指由式 (3.14) 定义多面体的空间。在模型空间中,来自两多面体的每个包围面 p 映射到对偶空间中的一个点 \(p^{'}\) 。该映射关系如下:
\[p \Rightarrow p^{'}=(\frac{a}{d},\frac{b}{d},\frac{c}{d})\]式中, a 、 b 、 c 以及 d 是包围面 p 的平面方程参数。
在对偶空间中求解所有 \(p^{'}\) 的凸包。鉴于新原点在接触重叠内部, \(p^{'}\) 总是存在的。在模型空间中,包围面离新原点越远,在对偶空间中对应的点将离新原点越近。因此,所有对偶点的凸包对应接触重叠。
由上一步获得的凸包按下述映射关系映射回模型空间:
\[q^{'} \Rightarrow q=(\frac{a^{'}}{d^{'}},\frac{b^{'}}{d^{'}},\frac{c^{'}}{d^{'}})\]式中, \(q^{'}\) 为在对偶空间中的凸包包围面; \(a^{'}\) 、 \(b^{'}\) 、 \(c^{'}\) 以及 \(d^{'}\) 是 \(q^{'}\) 的平面方程参数; \(q\) 是模型空间中接触重叠的一点。在模型空间中的所有接触重叠点 \(q\) 的凸包即为所需求解的接触重叠多面体。
根据所求得的接触重叠多面体,通过经典的计算几何算法便可很容易地求解接触方向和接触点。在此,我们引入接触交线来确定接触法向。接触交线是两接触颗粒表面的相交线,参见 图 3.3 或 图 3.5 。图 3.5 显示了两接触多面体(见 图 3.3 )的相交多面体。针对接触交线的所有组成线段,利用最小二乘法拟合出一个拟合平面,并假设该拟合平面的法向为接触法向,与该法向正交的方向为切向方向。值得注意的是,此处的切向方向严格地说是切向方向所在平面(切平面),具体的某一接触切向与两颗粒在该切向平面的相对位移有关。对于球形颗粒,接触交线严格地位于拟合平面上,见 图 3.4 ,然而对于多面体颗粒则不然。此外,可假设重叠部分(多面体)的质心作为接触点,亦即接触力的作用点。值得指出的是,上述接触法向和接触点的定义是非常近似的,因为两多面体的重叠部分(见 图 3.3 是不规则的,并且实际上存在多个接触点,比如在面面接触或面边接触处。此外,在多数情况下,接触点并不落在拟合平面上。
3.3.4. 体刚度接触模型¶
接触刚度模型,作为DEM中常用的接触模型,定义了接触力 \(F\) 与相对位移 \(\delta\) 之间的弹性关系,见式 (3.16) 。为方面描述以及建模,接触力通常被分为两正交分量:接触平面上的切向接触力 \(F_t\) 和接触平面法线方向的法向接触力 \(F_n\) ,如 图 3.3 所示。需要指出的是,接触平面被认为是由两多面体的相交曲线的最小二乘拟合所得 [3] 。
式中, \(K\) 为接触刚度,由接触颗粒的材料特性决定。如果接触刚度 \(K\) 在整个计算模拟过程中为常数,那么式 (3.16) 定义了一个线弹性接触模型。本文中的接触刚度 \(K\) 由式 (3.17) 给出,其中,上标A和B表示相接触的两个颗粒。
通常,式 (3.16) 中的接触重叠 \(\delta\) 为嵌入深度。此处,采用一个适用于任意颗粒形状的法向接触模型。如式 (3.18) 所示,法向接触力与接触重叠体积相关。该法向接触模型已被其他学者 [3, 5, 8, 9] 使用。
式中, \(K_n\) [N/m \(^3\) ]为接触法向刚度(体积刚度),由式 (3.17) 给出; \(v_c\) [m \(^3\) ]为接触重叠体积,其详细计算参见上一小节。
此外,采用最常用的切向接触模型,如下:
式中, \(K_t\) [N/m]为接触切向刚度; \(\Delta u\) 与 \(\Delta F_t\) 分别为当前时步切向接触位移增量和切向接触力增量。
库伦条件或滑动摩擦模型用于确定接触的滑动。当 \(F_t\) 大于 \(\tan\phi_\mu\cdot F_n\) (其中 \(\phi_\mu\) 为滑动摩擦角)时,接触发生滑动,此时 \(F_t\) 须减小并维持 \(\tan\phi_\mu\cdot F_n\) 。需要说明的是,鉴于滚动摩擦的影响相对较小 [6] ,本文模型不涉及滚动摩擦。
3.3.5. 参考文献¶
C. W. Boon, G. T. Houlsby, and S. Utili. A new algorithm for contact detection between convex polygonal and polyhedral particles in the discrete element method. Computers and Geotechnics, 44:73–82, June 2012.
P. A. Cundall. Formulation of a three-dimensional distinct element model—Part i. a scheme to detect and represent contacts in a system composed of many polyhedral blocks. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 25(3):107–116, June 1988.
Jan Eliáš. Simulation of railway ballast using crushable polyhedral particles. Powder Technology, 264:458–465, September 2014.
Oliver Günther and Eugene Wong. A dual approach to detect polyhedral intersections in arbitrary dimensions. BIT Numerical Mathematics, 31(1):2–14, March 1991.
CHEN Jian, Alexander SCHINNER, and Hans-Georg MATUTTIS. Discrete element simulation for polyhedral granular particles. Theoretical and Applied Mechanics Japan, 59:335–346, 2010.
Stuart Mack, Paul Langston, Colin Webb, and Trevor York. Experimental validation of polyhedral discrete element model. Powder Technology, 214(3):431–442, December 2011.
David E. Muller and Franco P. Preparata. Finding the intersection of two convex polyhedra. Theoretical Computer Science, 7(2):217–236, 1978.
Benjamin Nassauer and Meinhard Kuna. Contact forces of polyhedral particles in discrete element method. Granular Matter, 15(3):349–355, 2013.
Benjamin Nassauer, Thomas Liedke, and Meinhard Kuna. Polyhedral particles for the discrete element method. Granular Matter, 15(1):85–93, 2013.
E. G. Nezami, Y. M. A. Hashash, D. W. Zhao, and J. Ghaboussi. A fast contact detection algorithm for 3-D discrete element method. Computers and Geotechnics, 31(7):575–587, 2004.