4.4. DEMPM基本框架

SudoSim-DEMPM 为 SudoSim 系列的多尺度模块，该模块基于 MPM2D 和 GODEM，旨在利用DEM RVE替代唯象的应力-应变本构，实现颗粒材料的跨尺度求解。SudoSim-DEMPM 继承了 MPM2D 力学、热学、多尺度及相变求解框架，同时继承了 GODEM 的球形及非球颗粒模拟架构，实现了更为丰富的颗粒材料各向异性、非共轴性以及多物理场跨尺度的模拟。

SudoSim-DEMPM 利用MPM来求解宏观尺度边值问题，在应力更新阶段，由RVE来替代传统的材料本构模型，来表征砂土材料的应力应变关系，拓扑结构参见 图 4.7 。

• MPM2D : 大变形问题的建模、边界条件设置以及求解。

• GODEM: 速度梯度到应力的求解，以及多物理场状态量求解。

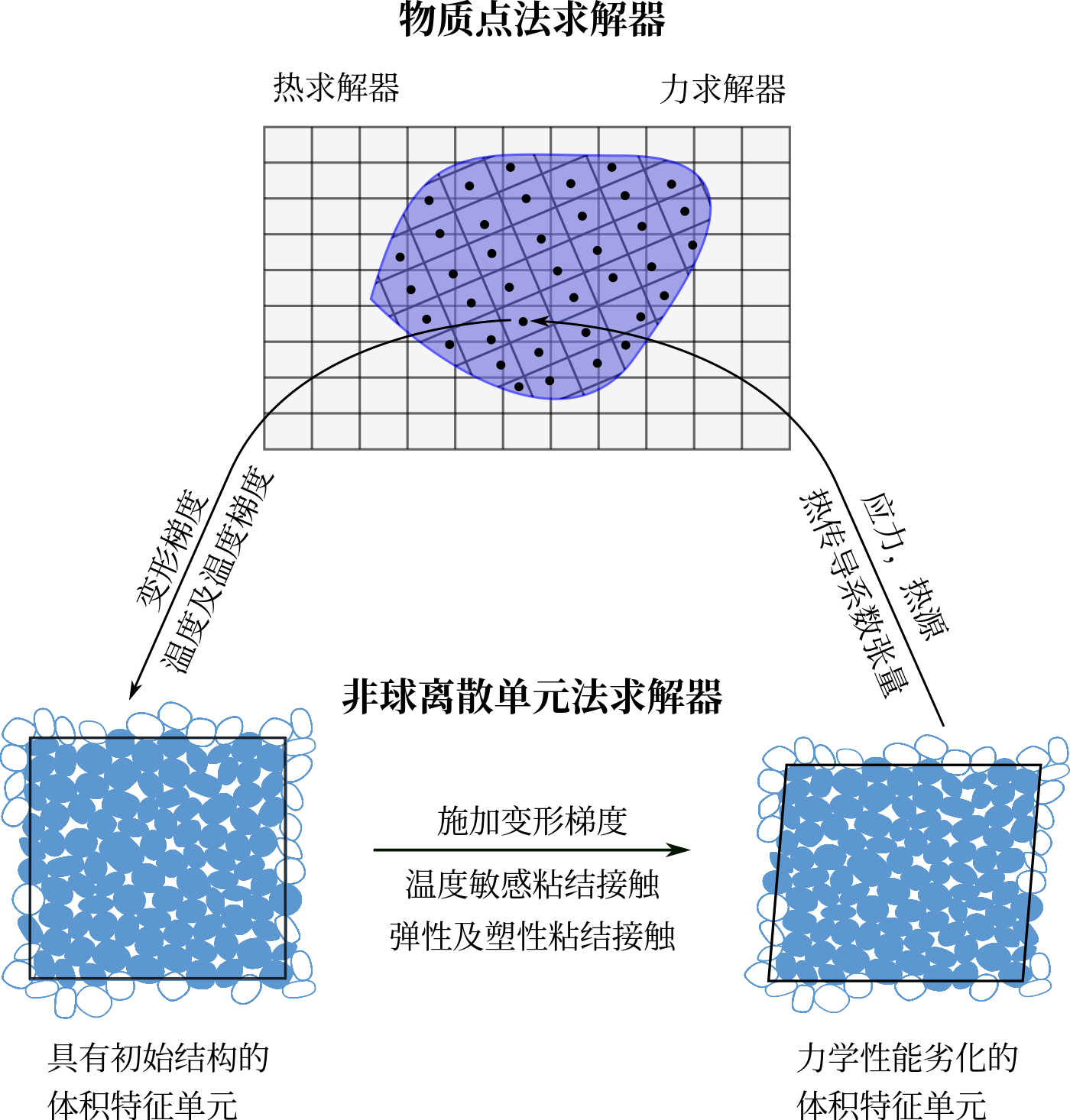
图 4.7 多尺度框架拓扑结构图

4.5. 周期边界与现时构型

多尺度求解依赖于宏观的变形梯度到细观应力的映射。

4.5.1. 变形梯度及应力

• 欧拉坐标系（ \(x_i\) ）和拉格朗日坐标系（ \(X_i\) ）的变换规则：

(4.12)\[\begin{split}x_i & = H_{ij}X_j \\ X_j & = H^{-1}_{jk}x_k\end{split}\]

• 现时构型全导数：

(4.13)\[\dot{x}_i = \underbrace{\dot{H}_{ij}X_j}_{v_{hi}} + \underbrace{H_{ij}\dot{X}_j}_{v_{fi}}\]

• 物质点宏观速度梯度：

(4.14)\[\mathbf{L}_{p}^{t + \Delta t} = \sum_{I} \nabla \phi_{I}(\mathbf{x}_{p}^{t}) \mathbf{v}_{I}^{t + \Delta t}\]

• 颗粒均质化应力

(4.15)\[\sigma_{ij} = \frac{1}{V}\sum_{c\in V}f_i^{c}b_j^{c} + \frac{1}{V}\sum_{p'\in V}m_{p'}v_{fi}^{p'}v_{fj}^{p'}\]

4.5.2. 弹塑性损伤接触劣化

• 非胶结模型不考虑胶结作用的颗粒间接触，力-位移关系如下：

  (4.16)\[\begin{split}\mathbf{f}^n =& -k_n \mathbf{u}^n\\ \Delta \mathbf{f}^t =& -k_t \delta \mathbf{u}^t \\ |\mathbf{f}^t| \leq & \mu |\mathbf{f}^n|\end{split}\]

• 刚性胶结模型考虑胶结作用，但胶结的破裂准则为脆性：

  (4.17)\[\begin{split}\Vert\mathbf{f}^n\Vert > F_{nb},& \quad{} F_{nb} = \beta_b c_n \hat{r}^2 \\ \Vert\mathbf{f}^t\Vert > F_{tb},& \quad{} F_{tb} = \beta_b c_t \hat{r}^2\end{split}\]

• 弹塑性损伤胶结模型考虑延性发展的接触劣化：

  屈服函数为，

  (4.18)\[\begin{split}f &= F_{n}\tan(\phi) - F_{tb}(1-H) \\ &+ \sqrt{(1-H)^{2}(F_{tb}-F_{nb}\tan(\phi))^{2} + (\lambda_{1} F_{t})^{2}}\end{split}\]

  流动法则为，

  (4.19)\[\begin{split}g = F_{t}^{2} - ((1-H)F_{tb} - F_{n}\tan(\psi))^{2} \\ - (1-H)^{2}(F_{tb} - F_{nb}\tan(\psi))^{2}\end{split}\]

  接触劣化状态更新为，

  (4.20)\[H = 1 - e^{-(\lambda_{2}^{2} + \lambda_{3}^{2})}\]

• 迭代过程为：

  

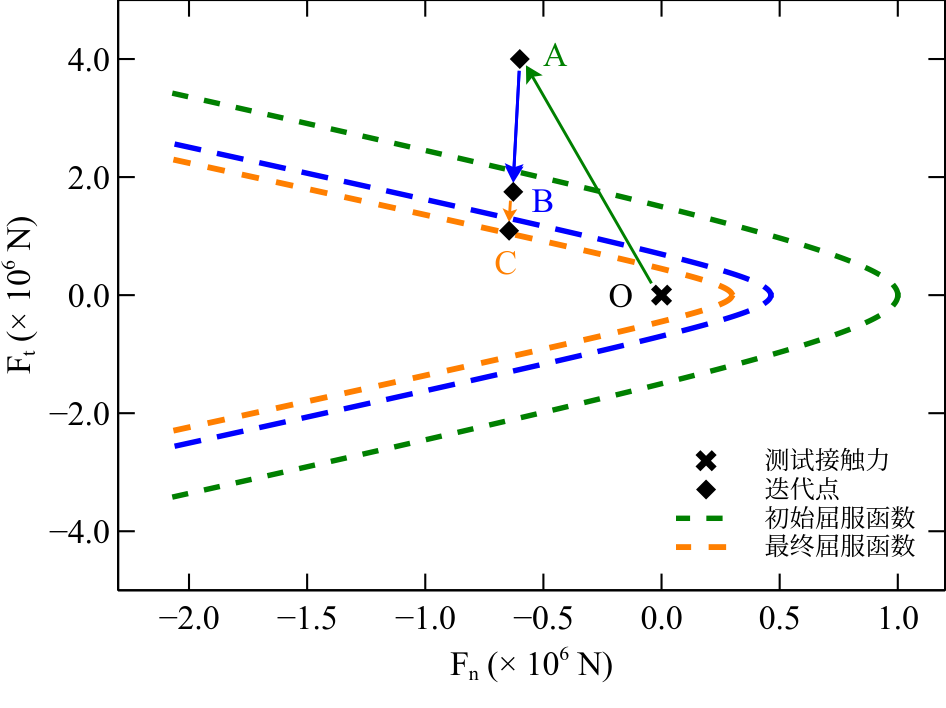
  图 4.8 弹塑性塑性损伤粘结本构迭代求解示意图

粘结本构均可退化为非粘结本构，且粘结本构的强度因子可考虑热力学响应。