8.2. 运行一个简单的模拟¶
该示例模拟了一个自由落体的球体掉在地面的过程。该例子对应的 Python 脚本名字为: ‘example0.py’, 你可以选择把该例子的工作路径设置为 (例如, /home/xxx/example’)。打开命令行并键入 ‘sudodem3d example0.py’ 来运行该例子。如果当前命令行路径不在例子工作路径下,你可能需要输入相对路径来指向正确的例子所处文件夹。
- 导入基础模块
1# module utils has some auxiliary functions 2from sudodem import utils
- 定义球体的材料
1mat = RolFrictMat(label="mat1",Kn=1e8,Ks=7e7,frictionAngle=math.atan(0.0),density=2650) # material 1 for particles 2wallmat1 = RolFrictMat(label="wallmat1",Kn=1e8,Ks=0,frictionAngle=0.) # material 2 for walls
- 将新定义的材料添加到模拟的材料数值中
O 可被认为是当前模拟的核心类。可以看到材料是 O 的一个属性, 所以我们可以用点操作来获取到对应的材料对象。在将材料添加到材料数组后我们可以通过材料的标签来获取其信息,参见下面墙体的材料定义。
1# materials is a list, i.e., a container for all materials involving in the simulations 2O.materials.append(mat) 3O.materials.append(wallmat1)
- 创建球体
1sp = sphere((0,0,10.0),1.0, material = mat) 2O.bodies.append(sp)
- 用无限大墙体来模拟地面
utils.wall 定义一面墙,其法线平行于全局笛卡尔坐标系的一个轴。 第一个参数(此处 = 0)指定墙的位置,通过关键字 axis(此处 = 2,axis 的 x、y、z 轴分别为 0、1、2)我们知道 墙沿着 z 轴,以 z = 0 为中心(0,由第一个参数指定); 第二个关键字 sense(这里 = 1,sense 可以分别为 -1、0、1,分别表示负边、正边和正边)指定墙的正边(即法线指向轴的正方向) 被激活,此时我们将计算颗粒与这面墙的相互作用; 最后一个关键字materials指定了这个墙的材质,我们为该关键字分配一个字符串(即wallmat1的标签),直接分配材质的对象(即RolFrictMat返回的wallmat1)也是可以的。
1ground = utils.wall(0,axis=2,sense=1, material = 'wallmat1') 2O.bodies.append(ground) # add the ground to the body container
- 使用PyRunner来周期性地执行函数。
1def record_data(): 2 # 打开文件 3 fout = open('data.dat','a') #create/open a file named 'data.dat' in append mode 4 #我们要记录球体的位置 5 p = O.bodies[0] # 球体已被追加到 O.bodies 列表中,我们可以使用相应的索引来访问它。 我们在O.bodies中总共添加了两个物体,球体是第一个,即索引为0。 6 # p 是球体的物体 7 # 作为一个实体对象,p 有几个属性,例如状态、材质,可以通过命令行中的 p.dict() 列出。 8 pos = p.state.pos # 获取球体的位置 9 # 我们将迭代次数和位置 (x,y,z) 写到文件 fout 中。 10 fout.write(f"{O.iter} {pos[0]} {pos[1]} {pos[2]}\n") 11 # 然后,关闭文件并释放资源 12 fout.close()
- 创建牛顿引擎来使得球体的运动遵循牛顿定律
设置局部阻尼为 0.1, 同时设置重力加速度为 9.8 m/s2,方向为z轴朝下。
1newton=NewtonIntegrator(damping = 0.1,gravity=(0.,0.0,-9.8),label="newton")
- 引擎数组是整个模拟的最核心的部分
在每个时步内,引擎依次运行来完成 DEM 一个完整的计算循环
1O.engines=[ 2# 首先,我们需要重置力容器以存储即将到来的接触力 3ForceResetter(), 4# 接下来,我们通过比较轴对齐包围盒 (AABB) 来排除那些绝对不接触的颗粒对,即粗略接触检测。 5InsertionSortCollider([Bo1_Sphere_Aabb(),Bo1_Wall_Aabb()],verletDist=0.2*0.01), 6# 然后,我们执行精细接触检测 7InteractionLoop( # 我们将循环所有潜在接触的颗粒对 8 # 对于不同颗粒形状,我们会调用相应的函数来计算接触几何, 9 # 例如Ig2_Sphere_Sphere_ScGeom()用于计算球-球的接触几何。 10 [Ig2_Sphere_Sphere_ScGeom(), Ig2_Wall_Sphere_ScGeom()], 11 # 我们将根据接触颗粒的物理属性计算接触的物理属性,例如接触刚度和摩擦系数。 12 [Ip2_RolFrictMat_RolFrictMat_RolFrictPhys()], 13 # 接下来,我们使用上述两步计算的信息(接触几何和物理属性)根据接触定律计算接触力。 14 [RollingResistanceLaw(use_rolling_resistance=False)] 15 ), 16newton, #最后,我们计算每个颗粒的加速度和速度并更新它们的位置。 17# 在每个时间步,我们都有一个 PyRunner 函数帮助侵入 DEM 循环并执行想要的任何操作, 18# 例如,更改颗粒状态、保存一些数据,或者在一定的运行时间后停止程序。 19PyRunner(command='record_data()',iterPeriod=10000,label='record',dead = False) 20]
- 设置时步
1O.dt = 1e-5
- 清空 data.dat 并写入文件头部信息
1fout = open('data.dat','w') # we open the file in a write mode so that the file will be clean 2fout.write('iter, x, y, z\n') # write a file head 3fout.close() # close the file
用户可通过如下两种方式来运行该模拟
- 执行命令
O.run()
或者设置时步来运行O.run(160000)
在 GUI 界面点击运行按钮来运行
在命令行中键入以下命令来运行脚本
1sudodem3d example0.py
多线程运行(例如, 使用2个线程)
sudodem3d -j2 example0.py
运行时所保存的数据如下所示:
iter, x, y, z
10000 0.0 0.0 9.95588676912
20000 0.0 0.0 9.82357353912
30000 0.0 0.0 9.60306030912
40000 0.0 0.0 9.29434707912
50000 0.0 0.0 8.89743384912
60000 0.0 0.0 8.41232061912
70000 0.0 0.0 7.83900738912
用户可以使用 gnuplot 来快速可视化模拟结果 (gnuplot 可通过在命令行键入以下命令来完成安装):
sudo apt install gnuplot
然后打开 gnuplot, 图 8.1 所示了 gnuplot 可视化的计算结果:
1$> gnuplot
2 gnuplot> plot 'data.dat' using ($1/10000):4; set xlabel 'iterations [x10000]'; set ylabel 'position z [m]'
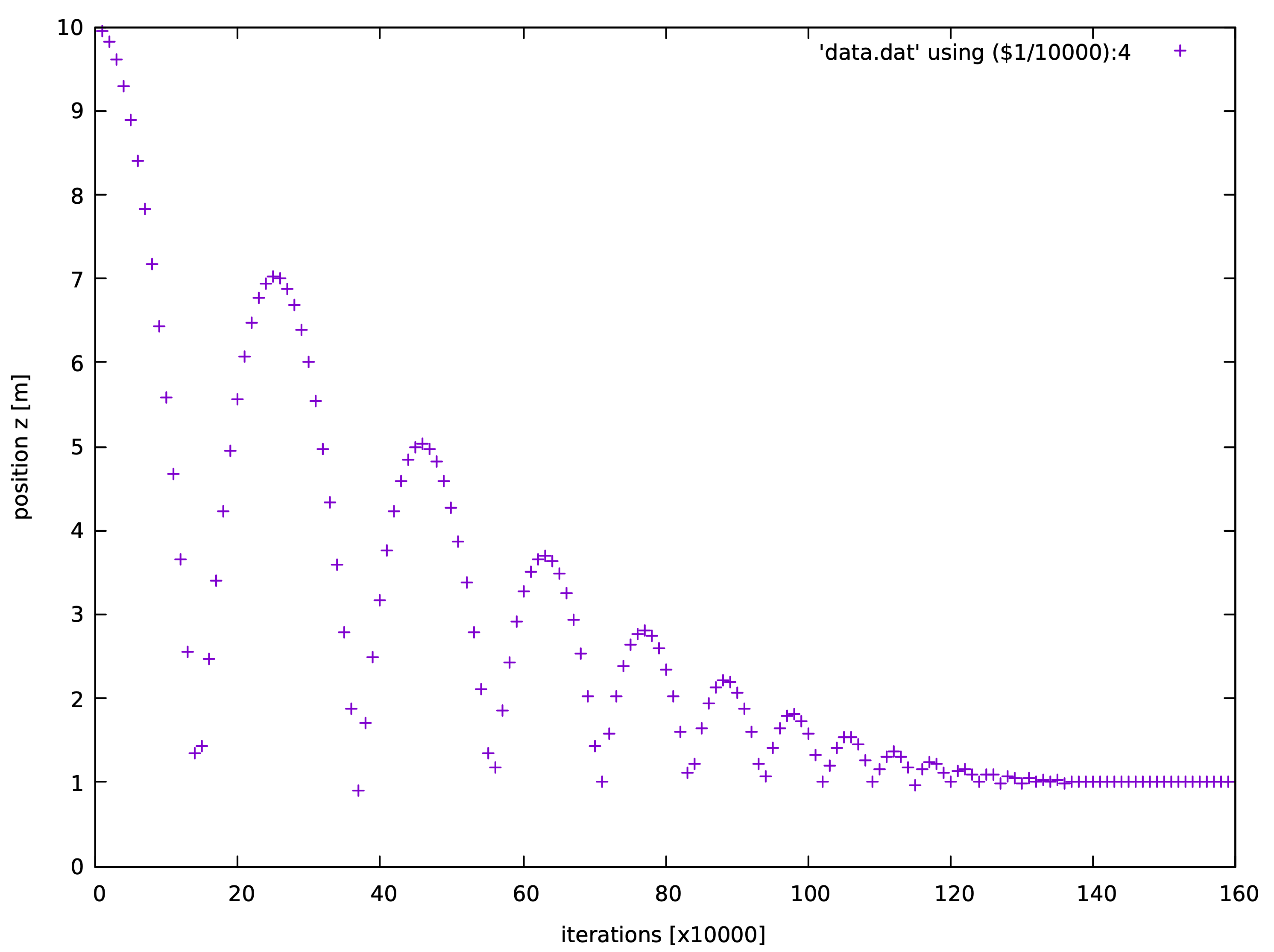
图 8.1 球体自由落体到地面的z方向坐标变化¶