3.4. 超椭球离散元模型

3.4.1. 超椭球颗粒

3.4.1.1. 基本定义

超椭球面是一类特殊的闭合超二次曲面，能够表达丰富的几何形状。在局部笛卡尔坐标系下，超椭球的表面方程可以定义为 [2] ：

(3.20)\[(|\frac{x}{a}|^{\frac{2}{\epsilon_1}} + |\frac{y}{b}|^{\frac{2}{\epsilon_2}})^{\frac{\epsilon_1}{\epsilon_2}} + |\frac{z}{c}|^{\frac{2}{\epsilon_2}} = 1\]

其中，\(a\) 、 \(b\) 以及 \(c\) 分别是在x、y和z轴方向上的半长轴长度， \(\epsilon_i (i=1,2)\) 是确定颗粒边缘尖锐程度的形状参数。 感兴趣的读者可在文献 [3, 8] 中找到超椭球的其他类似定义。本文主要研究凸形状，其对应的 \(\epsilon_i\) 在 \((0,2)\) 之间。如 图 3.6 所示，改变 \(\epsilon_i\) 可以得到多种形状。 特别地， \(\epsilon_i \rightarrow 0\) 时对应立方体形状，而 \(\epsilon_i \rightarrow 2\) 时对应八面体形状。

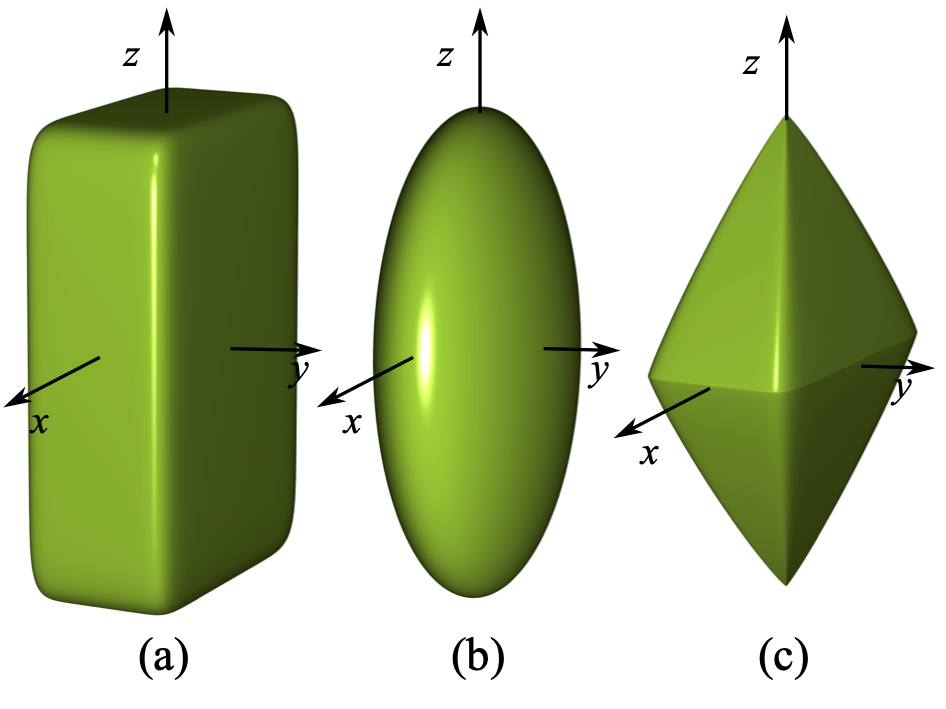
图 3.6 轴长为 \(a=2\) 、 \(b=1\) 、 \(c=3\) 的超椭球：(a) \(\epsilon_1 = \epsilon_2 = 0.2\) ；(b) \(\epsilon_1 = \epsilon_2 = 1.0\) ；(c) \(\epsilon_1 = 0.2\) ， \(\epsilon_2 = 1.8\)

3.4.1.2. 主要几何参量

以下给出了本模型中涉及到的超椭球的一系列重要的几何参量，如体积、主惯性矩等。 超椭球的体积由下式给出:

(3.21)\[V = 2AB(\frac{1}{2}\epsilon_1+1, \epsilon_1)B(\frac{1}{2}\epsilon_2, \frac{1}{2}\epsilon_2)\]

式中， \(A\) 等于 \(abc\epsilon_1\epsilon_2\) ； \(B(x, y)\) 为贝塔函数，定义为

\[B(x, y) = 2\int_0^{\frac{\pi}{2}}\mathrm{sin}^{2x-1}\phi \mathrm{cos}^{2y-1}\phi d\phi = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}\]

其中， \(\Gamma(x)\) 为伽马函数。 超椭球的主惯性矩为：

(3.22)\[\begin{split}I_1 &= I_{xx} =\frac{1}{2} \rho A(b^2\beta_1 + 4c^2\beta_2) \\ I_2 &= I_{yy} = \frac{1}{2} \rho A(a^2\beta_1 + 4c^2\beta_2) \\ I_3 &= I_{zz} = \frac{1}{2} \rho A(a^2 + b^2)\beta_1\end{split}\]

式中， \(\rho\) 为材料密度, 参数 \(\beta_1\) 和 \(\beta_2\) 定义如下：

\[\begin{split}\left\{ \begin{array}{l@{}l} \beta_1 = B(\frac{3}{2}\epsilon_2, \frac{1}{2}\epsilon_2)B(\frac{1}{2}\epsilon_1, 2\epsilon_1 + 1)\\ \beta_2 = B(\frac{1}{2}\epsilon_2, \frac{1}{2}\epsilon_2 + 1)B(\frac{3}{2}\epsilon_1,\epsilon_1+1) \end{array} \right.\end{split}\]

3.4.1.3. 超椭球主曲率

给定超椭球的参数方程为：

\[\begin{split}\mathbf{r}(\theta,\phi)= \begin{bmatrix} \mathrm{Sign}(\cos\theta)r_x|\cos\theta|^{\epsilon_1}|\cos\phi|^{\epsilon_2} \\ \mathrm{Sign}(\sin\theta)r_y|\sin\theta|^{\epsilon_1}|\cos\phi|^{\epsilon_2} \\ \mathrm{Sign}(\sin\phi)r_z|\sin\phi|^{\epsilon_2} \end{bmatrix}\end{split}\]

且 \(\theta \in [0,2\pi),\phi \in [-\frac{\pi}{2},\frac{\pi}{2}]\) 。其中，\(r_x\) 、 \(r_y\) 和 \(r_z\) 为局部坐标系下在主轴方向的半长轴； \(\mathrm{Sign}(x)\) 表示符号函数，定义如下：

(3.23)\[\begin{split}\mathrm{Sign}(x) = \begin{cases} -1 & \text{if} \quad x < 0, \\\\ 0 & \text{if} \quad x = 0, \\\\ 1 & \text{if} \quad x > 0. \end{cases}\end{split}\]

因此，参数方程的一阶和二阶导数为：

\[\begin{split}\mathbf{r}_{\theta}= \begin{bmatrix} -\mathrm{Sign}(\cos\theta)r_x\epsilon_1|\cos\theta|^{\epsilon_1 -2}|\cos\phi|^{\epsilon_2}\cos\theta\sin\theta \\\\ \mathrm{Sign}(\sin\theta)r_y\epsilon_1|\sin\theta|^{\epsilon_1-2}|\cos\phi|^{\epsilon_2}\cos\theta\sin\theta \\\\ 0 \end{bmatrix}\end{split}\]

\[\begin{split}\mathbf{r}_{\phi}= \begin{bmatrix} -\mathrm{Sign}(\cos\theta)r_x\epsilon_2|\cos\theta|^{\epsilon_1}|\cos\phi|^{\epsilon_2-2}\cos\phi\sin\phi \\\\ -\mathrm{Sign}(\sin\theta)r_y\epsilon_2|\sin\theta|^{\epsilon_1}|\cos\phi|^{\epsilon_2-2}\cos\phi\sin\phi \\\\ \mathrm{Sign}(\sin\phi)r_z\epsilon_2|\sin\phi|^{\epsilon_2-2}\cos\phi\sin\phi \end{bmatrix}\end{split}\]

\[\begin{split}\mathbf{r}_{\theta\phi}=\frac{\sin2\theta\sin2\phi}{4} \begin{bmatrix} \mathrm{Sign}(\cos\theta)r_x\epsilon_1\epsilon_2|\cos\theta|^{\epsilon_1-2}|\cos\phi|^{\epsilon_2-2} \\ -\mathrm{Sign}(\sin\theta)r_y\epsilon_1\epsilon_2|\sin\theta|^{\epsilon_1-2}|\cos\phi|^{\epsilon_2-2} \\ 0 \end{bmatrix}\end{split}\]

\[\begin{split}\mathbf{r}_{\theta\theta}= \begin{bmatrix} \mathrm{Sign}(\cos\theta)r_x\epsilon_1|\cos\theta|^{\epsilon_1-2}|\cos\phi|^{\epsilon_2}(\epsilon_1\sin^2\theta-1) \\\\ \mathrm{Sign}(\sin\theta)r_y\epsilon_1|\sin\theta|^{\epsilon_1-2}|\cos\phi|^{\epsilon_2}(\epsilon_1\cos^2\theta-1)\\\\ 0 \end{bmatrix}\end{split}\]

\[\begin{split}\mathbf{r}_{\phi\phi}= \begin{bmatrix} \mathrm{Sign}(\cos\theta)r_x\epsilon_2|\cos\theta|^{\epsilon_1}|\cos\phi|^{\epsilon_2-2}(\epsilon_2\sin^2\phi-1) \\\\ \mathrm{Sign}(\sin\theta)r_y\epsilon_2|\sin\theta|^{\epsilon_1}|\cos\phi|^{\epsilon_2-2}(\epsilon_2\sin^2\phi-1)\\\\ \mathrm{Sign}(\sin\phi)r_z\epsilon_2|\sin\phi|^{\epsilon_2-2}(\epsilon_2\cos^2\phi-1) \end{bmatrix}\end{split}\]

超椭球表面的外法线单位向量为：

\[\mathbf{n}=\frac{\mathbf{r}_{\theta} \times \mathbf{r}_{\phi}}{| \mathbf{r}_{\theta}\times \mathbf{r}_{\phi} |}\]

式中， \(\times\) 表示向量叉乘， \(|\quad|\) 表示向量模。

第一基本形式系数：

\[E=\mathbf{r}_{\theta}\cdot \mathbf{r}_{\theta} \quad{} F=\mathbf{r}_{\theta}\cdot \mathbf{r}_{\phi} \quad{} G=\mathbf{r}_{\phi}\cdot \mathbf{r}_{\phi}\]

其中，’ \(\cdot\)’ 表示向量点乘。 第二基本形式系数：

\[L=\mathbf{r}_{\theta\theta}\cdot \mathbf{n} \quad M=\mathbf{r}_{\theta\phi}\cdot \mathbf{n}=0 \quad N=\mathbf{r}_{\phi\phi}\cdot \mathbf{n}\]

高斯曲率：

\[K=\frac{LN}{EG-F^2}\]

平均曲率：

\[H=\frac{EN+GL}{2(EG-F^2)}\]

主曲率：

\[\rho_{I}=H+\sqrt{H^2-K} \quad \rho_{II}=H-\sqrt{H^2-K}\]

3.4.1.4. 几何变换函数

给定超椭球表面上一点的局部球坐标 \((\theta, \phi)\) ，对应的笛卡尔坐标 \((x, y, z)\) 可由如下函数 \(\mathbb{F}_1\) 获取：

(3.25)\[\begin{split}\begin{aligned} x =& \mathrm{Sign}(\mathrm{cos}(\theta))a|\mathrm{cos}(\theta)|^{\epsilon_1} |\mathrm{cos}(\phi)|^{\epsilon_2}\\ y =& \mathrm{Sign}(\mathrm{sin}(\theta))b|\mathrm{sin}(\theta)|^{\epsilon_1} |\mathrm{cos}(\phi)|^{\epsilon_2}\\ z =& \mathrm{Sign}(\mathrm{sin}(\phi))c|\mathrm{sin}(\phi)|^{\epsilon_2} \end{aligned}\end{split}\]

给定超椭球表面上一法向量 \((n_x, n_y, n_z)\) ，对应的局部球坐标 \((\theta, \phi)\) 可由如下函数 \(\mathbb{F}_2\) 获取：

(3.25)\[\begin{split}\begin{aligned} \theta = \mathrm{atan2}(\mathrm{Sign}(n_y)|b n_y|^{\frac{1}{2 - \epsilon_1}}, \mathrm{Sign}(n_x)|an_x|^{\frac{1}{2 - \epsilon_1}}) \\\\ \phi = \mathrm{atan2}(\mathrm{Sign}(n_z)|cn_z|\mathrm{cos}(\theta)|^{2 - \epsilon_2}|^{\frac{1}{2 - \epsilon_2}}, |an_x|^{\frac{1}{2 - \epsilon_2}}) \end{aligned}\end{split}\]

式中， \(\mathrm{atan2}(x, y)\) 为 \(\frac{x}{y}\) 的反正切函数，取值区间为 \((-\pi, \pi]\) ； \(\mathrm{Sign}(x)\) 为符号函数，定义参见式 (3.23) 。

3.4.2. 接触计算

在DEM的每个循环时步中都要更新颗粒间的接触嵌入深度和接触的方向，以便获得更新的接触力。给定两个可能接触的相邻颗粒A和B，把来自两颗粒的可能的接触点分别记为 \(\mathbf{p}^A\) 和 \(\mathbf{p}^B\) ，对应的潜在接触嵌入向量记为 \(\mathbf{d} = (\mathbf{p}^B-\mathbf{p}^A)\) ，参见 图 3.7 (a)。根据公共法向概念 [5, 7] ，待求解的接触点须要使接触嵌入深度最小，并且须要同时满足以下约束条件：

1. 在接触点 \(\mathbf{p}^A\) 和 \(\mathbf{p}^B\) 的颗粒表面外法线单位向量 \(\mathbf{n}^A\) 和 \(\mathbf{n}^B\) 满足反向平行，并且与接触方向 \(\mathbf{c}\) 平行，即：

   (3.26)\[\mathbf{n}^A = -\mathbf{n}^B = \mathbf{c}\]

2. 潜在的接触嵌入向量 \(\mathbf{d}\) 与接触方向 \(\mathbf{c}\) 平行，即：

   (3.27)\[\mathbf{d} \times \mathbf{c} = \mathbf{0}\]

因此，找出目标接触点是一个最优化问题。如Wellmann等 [7] 所建议的，接触方向 \(\mathbf{c}\) 在局部球面坐标系中可用两个角度进行参数化描述，即：

\[\mathbf{c}(\alpha, \beta) = \mathrm{cos}\alpha\mathrm{cos}\beta \mathbf{i}+ \mathrm{sin}\alpha\mathrm{cos}\beta \mathbf{j}+ \mathrm{sin}\beta \mathbf{k}\]

其中， \(\mathbf{i}\) 、 \(\mathbf{j}\) 、 \(\mathbf{k}\) 是全局笛卡尔坐标系的单位基矢量。 因此，考虑式 (3.26) ，接触点可表示为：

\[\begin{split}\left\{ \begin{array}{ll} \mathbf{p}^A = \mathbf{T}^{-1}_A\mathbb{F}_1^A(\mathbb{F}_2^A(\mathbf{T}_A\mathbf{c}(\alpha, \beta))) + \mathbf{s}^A\\\\ \mathbf{p}^B = \mathbf{T}^{-1}_B\mathbb{F}_1^B(\mathbb{F}_2^B(-\mathbf{T}_B\mathbf{c}(\alpha, \beta))) + \mathbf{s}^B \end{array} \right.\end{split}\]

其中， \(\mathbf{T}\) 是从全局坐标系到颗粒局部坐标系的旋转矩阵， \(\mathbf{T}^{-1}\) 是其逆矩阵； \(\mathbf{s}\) 是颗粒在全局坐标系下的位置矢量； \(\mathbb{F}_1\) 和 \(\mathbb{F}_2\) 是颗粒局部坐标系中的两个几何变换函数，参见式 (3.25) 和 (3.25) 。 因此，寻找嵌入深度 \(||\mathbf{d}||\) 等价为求解以下带两个参数的无约束优化问题：

(3.28)\[\underset{\alpha, \beta}{\mathrm{min}}||\mathbf{d}|| = \underset{\alpha, \beta}{\mathrm{min}}||\mathbf{p}^B - \mathbf{p}^A||\]

本文采用Nelder-Mead单纯形算法 [6] 来获得鲁棒性的求解过程。值得注意的是，当式 (3.28) 达到全局最小值时， 式 (3.27) 自动满足 [7] 。

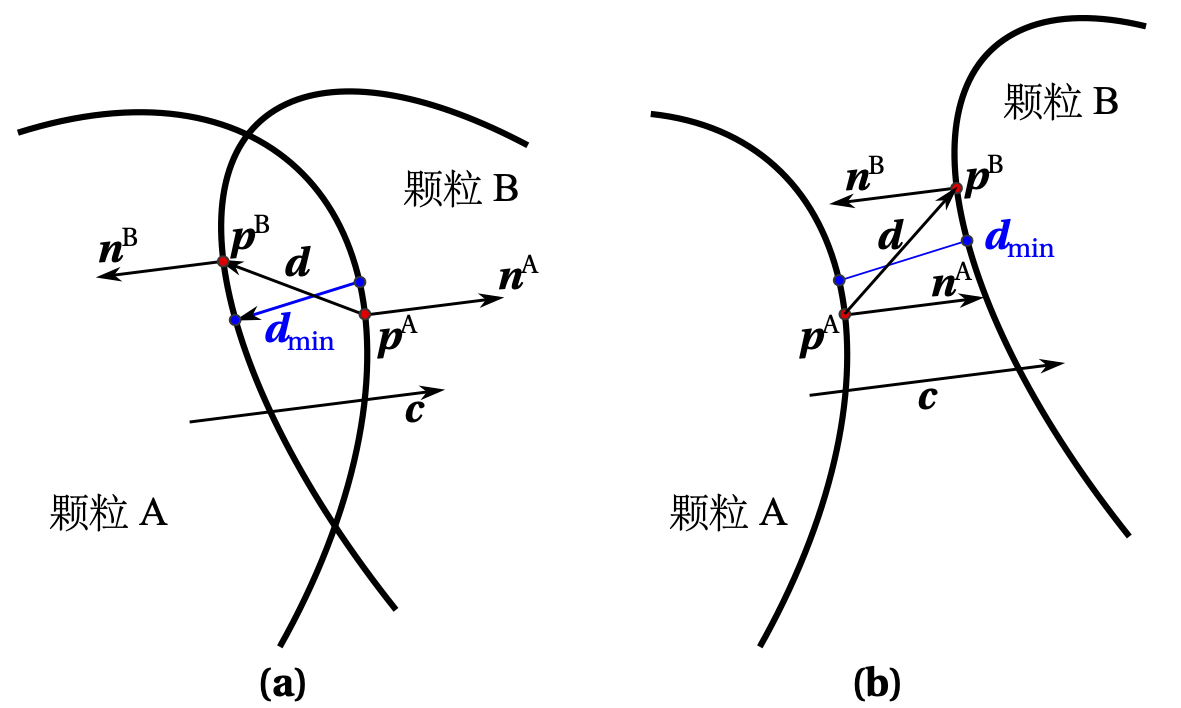
图 3.7 两接触颗粒(a)与两非接触颗粒(b)的最优化求解二维示意图

3.4.3. 接触检测

鉴于在每个时间步长都需要对大量的颗粒进行接触检测，可采用近似接触检测和精确接触检测的组合算法来加速接触检测过程。首先，采用两级近似接触检测方案。在第一级，轴对齐包围盒（AABB）算法（详见本章第二节）用于排除大部分不相互接触的颗粒对。鉴于超椭球的对称性，对于每个颗粒，使用固定尺寸的立方体AABB，即无需每一时步重新计算颗粒的AABB。然后，球形包围盒用于第二级的进一步筛除。对于剩下的可能存在相互接触的颗粒对，则需要进行精确接触检测，详见上一小节。需要强调的是，在优化求解过程中，可以在每次迭代时检查以下条件：

\[\mathbf{d} \cdot \mathbf{c} > 0\]

如果上述条件得到满足，那么所考察的颗粒对之间不存在接触 [7] ，参见 图 3.7 (b)，因而，可以排除当前的颗粒对，并终止该颗粒对的进一步接触检测。

3.4.4. 线刚度接触模型

DEM中假设颗粒是完全刚性但颗粒间可以发生重叠（所谓的软球模型） [4] ，参见 图 3.8 。 因此，可以根据给定接触本构模型和当前的重叠来计算排斥力。目前，学者们针对不同研究问题提出了各种接触模型。然而，由于线性弹簧模型 [1] 的简易性且对于非球颗粒可以显著提升计算效率（本文给出了详细讨论），其使用非常广泛。故本文的大部分数值模拟采用了这种模型，由下式给出：

\[\begin{split}\left\{ \begin{array}{l@{}l} F_n=\delta K_n\\\\ F_t=\mathrm{min}\{F_t^{'}-\Delta u K_t, \mu F_n\} \end{array} \right.\end{split}\]

其中， \(F_n\) 和 \(F_t\) 分别是法向和切向接触力； \(K_n\) 和 \(K_t\) 是对应的法向和切向接触刚度； \(\Delta u\) 是每个时间步长的接触切向位移增量； \(\delta\) 是接触处颗粒间的相互嵌入（重叠）深度； \(\mu\) 是颗粒间的摩擦系数； \(F_t^{'}\) 是上一个时间步长的切向接触力。需要指出的是，库仑条件（或滑动摩擦模型）被施加到切向接触力的计算。当接触形成时，切向接触力 \(F_t^{'}\) 被初始化为零。接触刚度 \(K_*\) （*`代表 :math:`n 或 \(t\) ）设置为两个接触颗粒材料刚度的调和平均值，见式 (3.29) ，其中上标A和B表示两个接触的颗粒。

(3.29)\[K_{*}=\frac{2K_{*}^AK_{*}^B}{K_{*}^A+K_{*}^B}\]

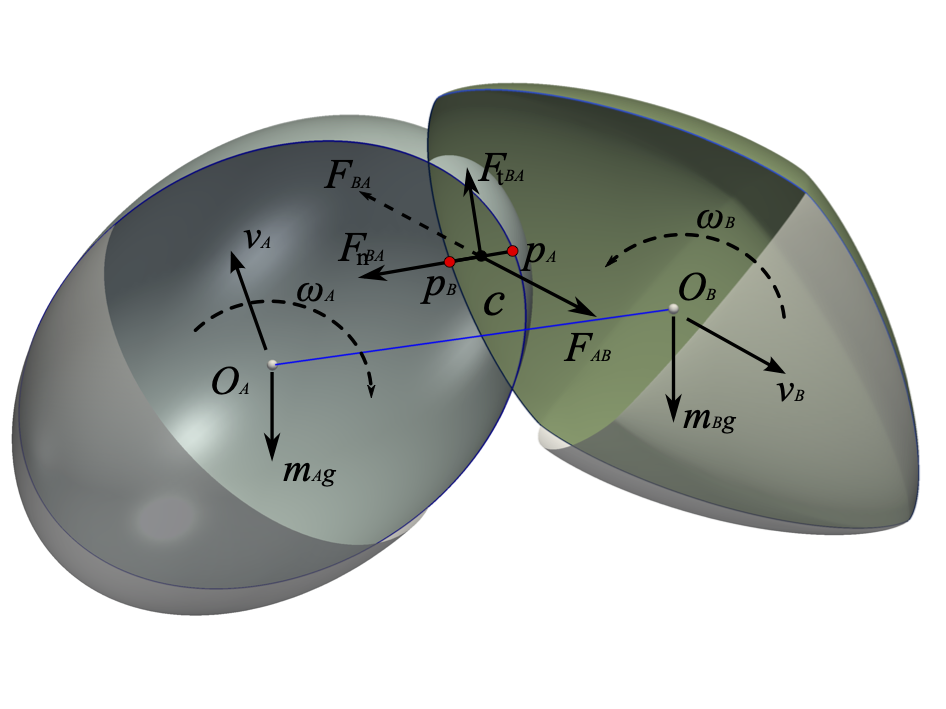
图 3.8 两接触超椭球颗粒的三维示意图

3.4.5. 参考文献

[1]

K Bagi. Statistical analysis of contact force components in random granular assemblies. Granular Matter, 5(1):45–54, 2003.

[2]

Alan H Barr. Superquadrics and angle-preserving transformations. IEEE Computer graphics and Applications, 1(1):11–23, 1981.

[3]

Paul W Cleary, Nick Stokes, and Jarrod Hurley. Efficient collision detection for three dimensional super-ellipsoidal particles. In Proceedings of 8th international computational techniques and applications conference CTAC97. Adelaide, 1997.

[4]

Peter A Cundall and Otto DL Strack. A discrete numerical model for granular assemblies. Géotechnique, 29(1):47–65, 1979.

[5]

KL Johnson. Contact Mechanics. Cambridge University Press, London, 1985.

[6]

Jeffrey C Lagarias, James A Reeds, Margaret H Wright, and Paul E Wright. Convergence properties of the nelder–mead simplex method in low dimensions. SIAM Journal on optimization, 9(1):112–147, 1998.

[7] (1,2,3,4)

Christian Wellmann, Claudia Lillie, and Peter Wriggers. A contact detection algorithm for superellipsoids based on the common-normal concept. Engineering Computations, 25(5):432–442, 2008.

[8]

John R Williams and Alex P Pentland. Superquadrics and modal dynamics for discrete elements in interactive design. Engineering Computations, 9(2):115–127, 1992.